Generalized golden sequences, a form of low discrepancy sequence or quasi random numbers See Martin Roberts: The Unreasonable Effectiveness of Quasirandom Sequences for background.

The d-dimensional sequence follows

x[i] = (x[i-1] .+ z) .% true, x[0] = x0

where

z = [ϕ[k]^(-i) for i in 1:d]

and ϕ[k] solves ϕ[k]^(d+1) = ϕ[k] + 1 (with ϕ[1] the golden mean.)

julia> GoldenSequence(0.0)[1]
0.6180339887498949

Shifted golden sequence starting in 0.5

julia>  GoldenSequence(0.5)[0]
0.5

julia>  GoldenSequence(0.5)[1]
0.1180339887498949

GoldenSequence returns an infinite iterator:

julia> collect(take(GoldenSequence(0.0), 10))
10-element Array{Float64,1}:
 0.0                
 0.6180339887498949
 0.2360679774997898
 0.8541019662496847
 0.4721359549995796
 0.09016994374947451
 0.7082039324993694
 0.3262379212492643
 0.9442719099991592
 0.5623058987490541

Random colors: Low discrepancy series are good choice for (quasi-) random colors

using Colors
n = 20
c = map(x->RGB(x...), (take(GoldenSequence(3), n))) # perfect for random colors

julia>  GoldenSequence(2)[1]
(0.7548776662466927, 0.5698402909980532)

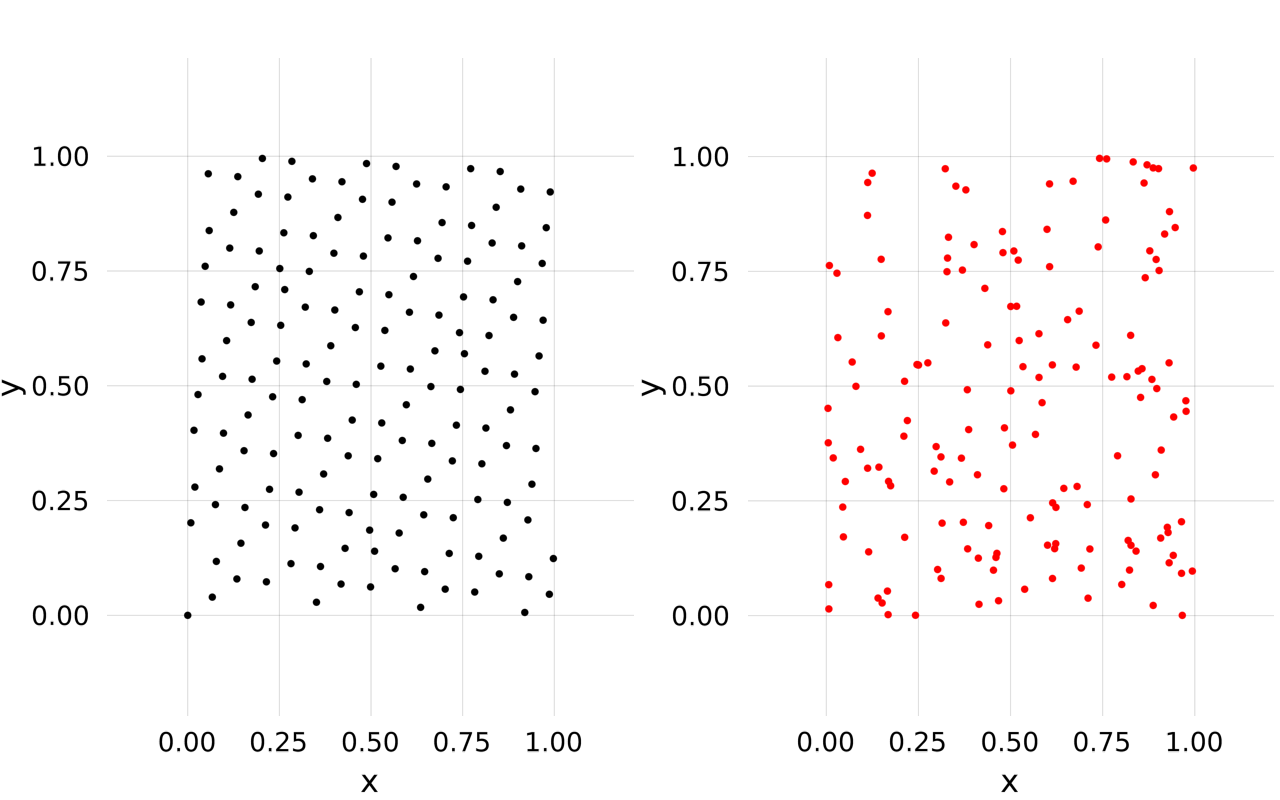
As low discrepancy series these number are well distributed (left), better than random numbers (right):

using Makie
n = 155
x = collect(Iterators.take(GoldenSequence(2), n))
p1 = scatter(x, markersize=0.02)
y = [(rand(),rand()) for i in 1:n]
p2 = scatter(y, markersize=0.02, color=:red)
vbox(p1, p2)

With a bit of effort, one can use Golden Sequences to generate spacefilling quasirandom sequences of cartesian indices. For example GoldenCartesianSequence((m[1], m[2])) will create a 2D Cartesian sequence corresponding to (approximate) samples of the Golden sequence in 1:m[1] x 1:m[2].

For that, GoldenCartesianSequence((m[1], ..., m[d])) will create full period linear congruential generators (LCG) x[i+1] = (x[i] + c[k]) % m[k] approximating phi[d]^[-k] by c[k]/m[k] such that c[k] and m[k] are coprime.

If m[1], ..., m[d] are coprime themselves, these LCG will have together period prod(m) and the sequence will be space filling, that is sort(collect(take(GoldenCartesianSequence(m), prod(m)))) == CartesianIndices(m)[:].

This means that if m[k] is the denominator of a good rational approximation c[k]//m[k] ≈ ϕ[d]^(-k), then the indices will be well distributed even for large i.

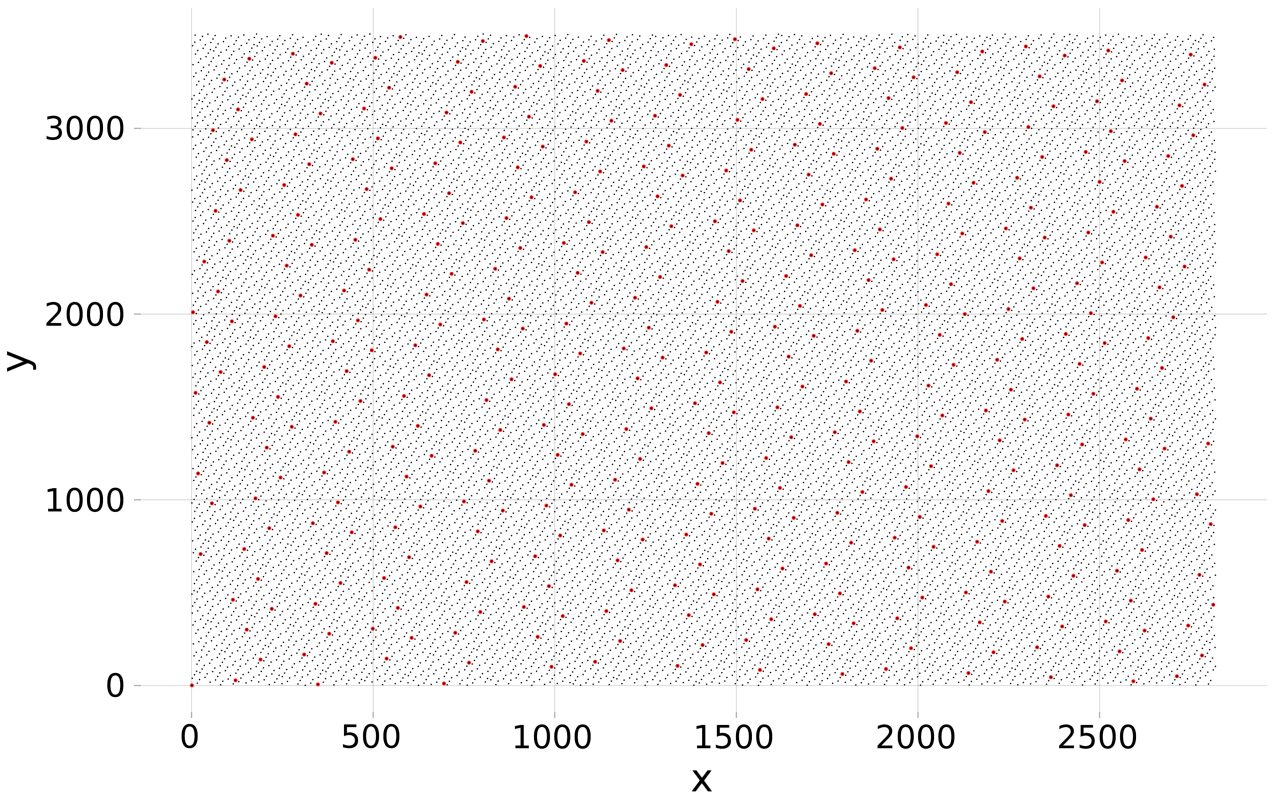
For example if m = (2819, 3508):

The image shows the fraction of the first 0.00005 (red) and the first 0.002 indices (black) in the GoldenCartesianSequence((2819, 3508)).

In short, good m are coprime denominators of fractions given by the function rationalize

d = 2
m = @. denominator(rationalize(GoldenSequences.phis[d]^(-(1:d)), tol=0.0000001))

julia> m
2-element Array{Int64,1}:
 2819
 3508

julia> gcd(m[1], m[2])
1

There are some connections here to Knuth's multiplicative hashing method

hash(i) = mod(i*2654435769, 2^32)

where 2654435769 is approximately 2^32*ϕ.

GoldenSequence(n::Int) # Float64 n-dimensional golden sequence
GoldenSequence(x0::Number) # 1-d golden sequence shifted by `x0`
GoldenSequence(x0) # length(x)-d golden sequence shifted/starting in 'x0'

Flower petals grow in spots not covering older petals, the new spot is at an angle given by the golden sequence.

using Colors
using Makie
n = 20
c = map(x->RGB(x...), (take(GoldenSequence(3), n))) # perfect for random colors
x = collect(take(GoldenSequence(0.0), n))
petals = [(i*cos(2pi*x), i*sin(2pi*x)) for (i,x) in  enumerate(x)]
scatter(reverse(petals), color=c, markersize=10*(n:-1:1))