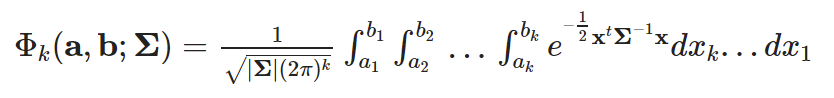Quasi-Monte-Carlo numerical computation of multivariate normal probabilities.

This function uses an algorithm given in the paper "Numerical Computation of Multivariate Normal Probabilities", in J. of Computational and Graphical Stat., 1(1992), pp. 141-149, by Alan Genz, WSU Math, PO Box 643113, Pullman, WA 99164-3113 Email : alangenz@wsu.edu

The primary references for the numerical integration are "On a Number-Theoretical Integration Method" H. Niederreiter, Aequationes Mathematicae, 8(1972), pp. 304-11, and "Randomization of Number Theoretic Methods for Multiple Integration" R. Cranley and T.N.L. Patterson, SIAM J Numer Anal, 13(1976), pp. 904-14.

Re-coded in Julia from the MATLAB function qsimvnv(m,r,a,b) Alan Genz is the author the MATLAB qsimvnv() function.

Alan Genz software website: http://archive.is/jdeRh Source code to MATLAB qsimvnv() function: http://archive.is/h5L37

import Pkg; Pkg.add("MvNormalCDF")

    mvnormcdf(dist::MvNormal, a, b; m::Integer = 1000*size(dist.Σ,1), rng = RandomDevice())

Computes the Multivariate Normal probability integral using a quasi-Monte-Carlo algorithm with m points for multivariate normal distributions (MvNormal)

Results will vary slightly from run-to-run due to the quasi-Monte-Carlo algorithm.

There is no covariance matrix Σ positive definite check.

Probability p is output with error estimate e.

⚠️ Check estimate e after integration.: Be very careful here! If e == 0 - results could be unstable or could be wrong (one of the reasons can be an ill-conditioned Σ matrix).

• dist::MvNormal: multivariate normal distributions from Distributions.jl
• a::AbstractVector: lower integration limit column vector
• b::AbstractVector: upper integration limit column vector
• m::Integer: number of integration points (default 1000*dimension)
• rng: random number generator

    mvnormcdf(μ::AbstractVector{<:Real}, Σ::AbstractMatrix{<:Real}, a::AbstractVector{<:Real}, b::AbstractVector{<:Real}; m::Integer = 1000*size(Σ,1), rng = RandomDevice())

Computes the Non-central Multivariate Normal probability integral with covariance matrix Σ and mean vector μ [x,...].

• μ::AbstractVector: vector of means
• Σ::AbstractMatrix: positive-definite covariance matrix of MVN distribution
• a::AbstractVector: lower integration limit column vector
• b::AbstractVector: upper integration limit column vector
• m::Integer: number of integration points (default 1000*dimension)
• rng: random number generator

Σ = [4 3 2 1; 3 5 -1 1; 2 -1 4 2; 1 1 2 5]
μ = zeros(4)
a = [-Inf; -Inf; -Inf; -Inf]
b = [1; 2; 3; 4]
m = 5000
(p,e) = mvnormcdf(μ, Σ, a, b; m=m)
#(0.605219554009911, 0.0015718064928452481)

     mvnormcdf(Σ::AbstractMatrix, a::AbstractVector, b::AbstractVector; m::Integer = 1000*size(Σ,1), rng = RandomDevice())

Computes the Multivariate Normal probability integral with covariance matrix Σ, mean [0,...].

Σ = [4 2; 2 3]
μ = [1; 2]
a = [-Inf; -Inf]
b = [2; 2]
(p,e) = mvnormcdf(Σ, a-μ, b-μ)
#(0.4306346895870772, 0.00015776288569406053)

    MvNormalCDF.qsimvnv!(Σ::AbstractMatrix{T}, a::AbstractVector{T}, b::AbstractVector{T}, m::Integer, rng) where T

Re-coded in Julia from the MATLAB function qsimvnv(m,r,a,b); mutate Σ, a, b. Computes the Multivariate Normal probability integral with covariance matrix Σ, mean [0,...].

• Genz, A. (1992). Numerical computation of multivariate normal probabilities. Journal of Computational and Graphical Statistics, 1, 141--150
• Genz, A. (1993). Comparison of methods for the computation of multivariate normal probabilities. Computing Science and Statistics, 25, 400--405

Idea was taken from this PR to StatsFuns.jl.

See discourse discussion here.

Thanks to @blackeneth.

QSIMVNV(m,r,a,b) and _chlrdr(r,a,b)

Copyright (C) 2013, Alan Genz, All rights reserved.

Redistribution and use in source and binary forms, with or without modification, are permitted provided the following conditions are met:

1. Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
2. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
3. The contributor name(s) may not be used to endorse or promote products derived from this software without specific prior written permission. THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.