julia> ]
pkg> add NSGAII
using NSGAII
n = 20 #Number of items
p1 = [77,94,71,63,96,82,85,75,72,91,99,63,84,87,79,94,90,60,69,62] #Coeffs objective 1
p2 = [65,90,90,77,95,84,70,94,66,92,74,97,60,60,65,97,93,60,69,74] #Coeffs objective 2
w = [80,87,68,72,66,77,99,85,70,93,98,72,100,89,67,86,91,79,71,99] #Items weights
c = 900 #Knapsack capacityThe four mandatory parameters of NSGAII are
- the size of the population
- the number of generations
- an initialization function
- an evaluation function
using Random: bitrand
using LinearAlgebra: dot
popsize = 100
nbgen = 200
init() = bitrand(n) #our genotype is a binary vector of size n, initialized randomly
z(x) = dot(x, p1), dot(x, p2) #and our objectives are the sum of the items we pickNow, this would be enough to run nsga-2 with
nsga_max(popsize, nbgen, z, init)
But we need to add the constraint that all items must fit in the knapsack.
For this we define a constraint-violation function that returns 0 only if the solution is feasible,
and a value > 0 otherwise.
function CV(x)
sumW = dot(x, w)
return sumW <= c ? 0 : sumW - c
end
#We can now call
result = nsga_max(popsize, nbgen, z, init, fCV = CV)result will be a vector of individuals.
The revelant fields of an individual indiv are :
- genotype :
indiv.x - objective values :
indiv.y - rank :
indiv.rank - constraint violation value :
indiv.CV
If the solutions are encoded as bitstrings, a 2-point crossover will be used by default, but we can define our own and assign it with the keyword fcross:
function one_point_crossover!(parent_a, parent_b, child_a, child_b)
n = length(parent_a)
cut = rand(1:n-1)
child_a[1:cut] .= parent_a[1:cut]
child_a[cut+1:n] .= parent_b[cut+1:n]
child_b[1:cut] .= parent_b[1:cut]
child_b[cut+1:n] .= parent_a[cut+1:n]
end
nsga_max(popsize, nbgen, z, init, fCV = CV, fcross = one_point_crossover!)For permutations genotypes, the default crossover is the PMX (Partially-Mapped Crossover)
The default mutation for a binary vector is the bitstring mutation where each bit has a probability 1/l to be flipped (where l is the length of the vector)
As with crossovers, we can define or own mutation operator and assign it with the keyword fmut. The probability of mutation can be changed with the keyword pmut.
Let's say we want our mutation to flip two random bits :
function two_bits_flip!(bits)
for i = 1:2
n = rand(1:length(bits))
bits[n] = 1 - bits[n]
end
end
nsga_max(popsize, nbgen, z, init, fCV = CV, fmut = two_bits_flip!, pmut = 0.2)For permutations genotypes, the default mutation randomly swaps two indices.
Starting solutions can be provided as a vector with the keyword seed, for example :
x1 = greedy(p1, w, c)
x2 = greedy(p2, w, c)
x3 = greedy(p1 .+ p2, w, c)
nsga_max(popsize, nbgen, z, init, fCV = CV, seed = [x1, x2, x3])Make sure the type of your seeds is the same as the one given by calling init() !
A plot function can be passed with the keyword fplot, by default the population is plotted at every generation but this can be changed with the keyword plotevery.
Example with PyPlot :
using PyPlot
function plot_pop(P)
clf() #clears the figure
P = filter(indiv -> indiv.rank == 1, P) #keep only the non-dominated solutions
plot(map(x -> x.y[1], P), map(x -> x.y[2], P), "bo", markersize = 1)
sleep(0.1)
end
nsga_max(popsize, nbgen, z, init, fCV = CV, fplot = plot_pop, plotevery = 5)You can use BinaryCoding(ϵ::Int, lb::Vector, ub::Vector) to encode real variables with a precision ϵ, and with lower and upper bounds lb and ub
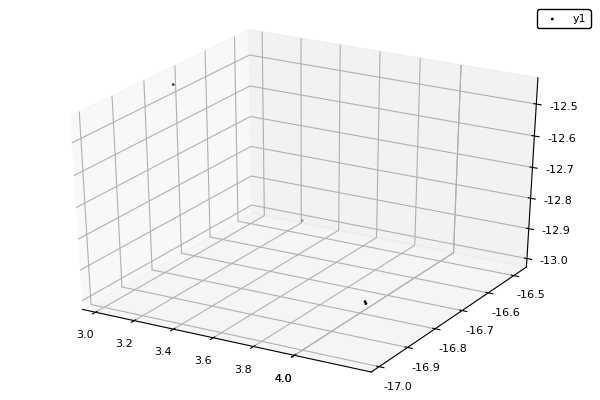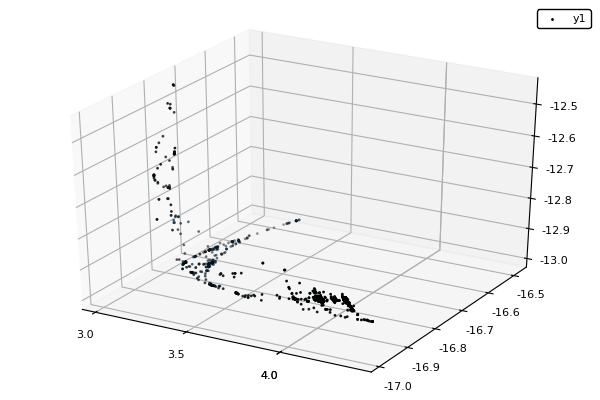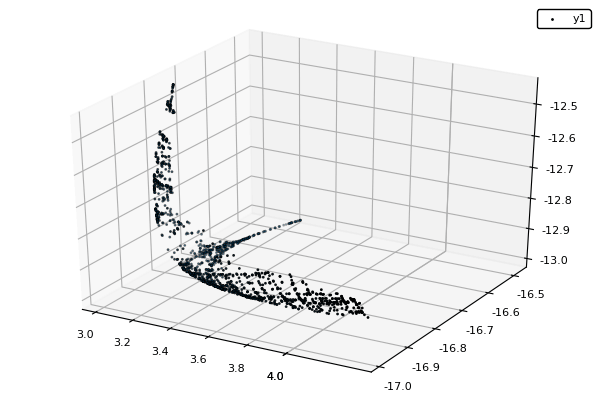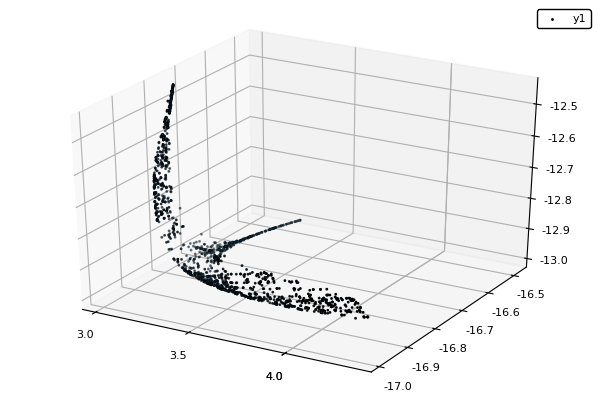
Example : MOP7 from Van Valedhuizen’s Test Suite
using NSGAII
using Plots: scatter3d
f1(x1,x2) = ((x1-2)^2)/2 + ((x2+1)^2)/13 + 3
f2(x1,x2) = ((x1+x2-3)^2)/36 + ((-x1+x2+2)^2)/8 - 17
f3(x1,x2) = ((x1+2x2-1)^2)/175 + ((-x1+2x2)^2)/17 - 13
z(x) = f1(x[1], x[2]), f2(x[1], x[2]), f3(x[1], x[2])
#Encodes two variables -400 <= x_i <= 400, with a precision of 1E-4
const bc = BinaryCoding(4, [-400, -400], [400, 400])
function plot_pop(pop)
pop = filter(indiv -> indiv.rank <= 1, pop) #keeps only the non-dominated solutions
scatter3d(map(x -> x.y[1], pop), map(x -> x.y[2], pop), map(x -> x.y[3], pop), markersize = 1) |> display
sleep(0.1)
end
nsga(500, 100, z, bc, seed = [[1.,-1.],[2.5,0.5],[0.5,0.25]], fplot = plot_pop)- The initialization function isn't needed anymore.
- The seed is passed as a vector of phenotypes, not a vector of genotypes, it is automatically encoded.
You can also use BinaryCoding(ϵ::Int, types, lb, ub) to encode a mix of integer, continuous or binary variables, with types a vector of symbols : ( :Int | :Cont | :Bin ).
The progress bar can be disabled by calling nsga(..., showprogress = false)