- All standard Young tableaux of a given shape:
julia> lambda = IPartition([3, 1])
IPartition(4, [3, 1])
julia> allSYTx(lambda)
3-element Vector{StandardYoungTableau}:
StandardYoungTableau(IPartition(4, [3, 1]), [[1, 3, 4], [2]])
StandardYoungTableau(IPartition(4, [3, 1]), [[1, 2, 4], [3]])
StandardYoungTableau(IPartition(4, [3, 1]), [[1, 2, 3], [4]])
- Count of all standard Young tableaux of a given shape:
julia> lambda = IPartition([4, 2])
IPartition(6, [4, 2])
julia> countSYTx(lambda)
9
- Uniform sampling of standard Young tableaux:
julia> randomSYT(lambda)
StandardYoungTableau(IPartition(6, [4, 2]), [[1, 2, 3, 6], [4, 5]])
- Robinson-Schensted(-Knuth) correspondence:
julia> P, Q = RS([3, 4, 1, 2])
(P = StandardYoungTableau(IPartition(4, [2, 2]), [[1, 2], [3, 4]]), Q = StandardYoungTableau(IPartition(4, [2, 2]), [[1, 2], [3, 4]]))
julia> P
StandardYoungTableau(IPartition(4, [2, 2]), [[1, 2], [3, 4]])
julia> Q
StandardYoungTableau(IPartition(4, [2, 2]), [[1, 2], [3, 4]])
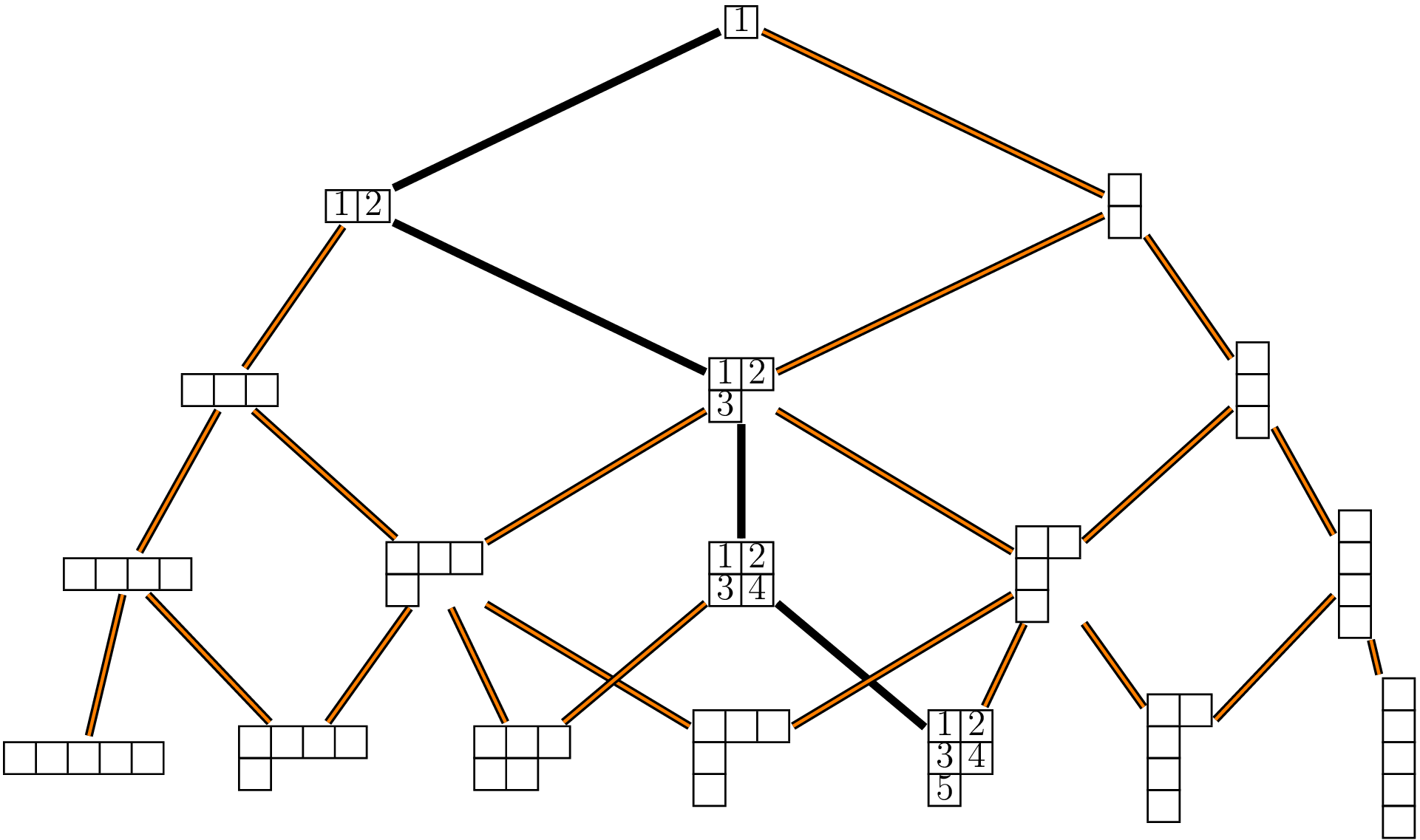
- Conversion to and from paths of integer partitions on the Young graph:
julia> y = StandardYoungTableau([[1,3,4], [2]])
StandardYoungTableau(IPartition(4, [3, 1]), [[1, 3, 4], [2]])
julia> path = SYT2YoungPath(y)
4-element Vector{IPartition}:
IPartition(1, [1])
IPartition(2, [1, 1])
IPartition(3, [2, 1])
IPartition(4, [3, 1])
julia> YoungPath2SYT(path)
StandardYoungTableau(IPartition(4, [3, 1]), [[1, 3, 4], [2]])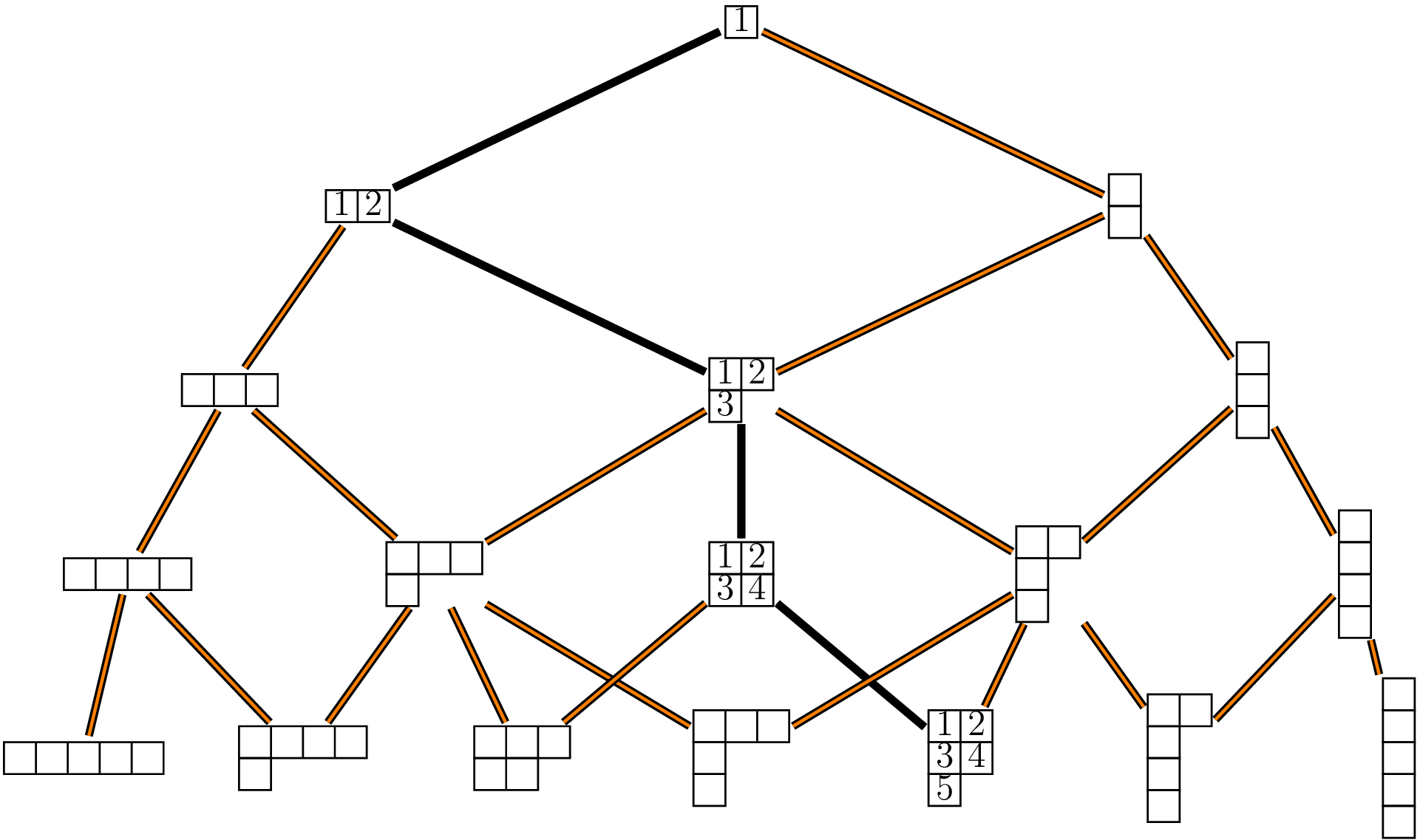
- Plancherel growth process:
julia> path = randomYoungPath(5)
5-element Vector{IPartition}:
IPartition(1, [1])
IPartition(2, [2])
IPartition(3, [2, 1])
IPartition(4, [3, 1])
IPartition(5, [3, 1, 1])
julia> YoungPath2SYT(path)
StandardYoungTableau(IPartition(5, [3, 1, 1]), [[1, 2, 4], [3], [5]])