IntelVectorMath.jl (formerly VML.jl)

This package provides bindings to the Intel MKL Vector Mathematics Functions. This is often substantially faster than broadcasting Julia's built-in functions, especially when applying a transcendental function over a large array. Until Julia 0.6 the package was registered as VML.jl.

Similar packages are Yeppp.jl, which wraps the open-source Yeppp library, and AppleAccelerate.jl, which provides access to macOS's Accelerate framework.

There is currently the following issue between the CompilerSupportLibraries_jll artifact, which is used for example by SpecialFunctions.jl, and MKL_jll. Unless MKL_jll is loaded first, there might be wrong results coming from a small number of function for particular input array lengths. If you are unsure which, if any, your used packages might load this artifact, loading IntelVectorMath as the very first package should be fine.

To install IntelVectorMath.jl run

julia> ] add IntelVectorMath

Since version 0.4 IntelVectorMath uses the MKL_jll artifact, which is shared with other packages uses MKL, removing several other dependencies. This has the side effect that from version 0.4 onwards this package requires at least Julia 1.3.

For older versions of Julia IntelVectorMath v0.3 downloads its own version of MKL and keeps only the required files in its own directory. As such installing MKL.jl or MKL via intel are no longer required, and may mean some duplicate files if they are present. However, this package will adopt the new artifact system in the next minor version update and fix this issue. In the event that MKL was not installed properly you will get an error when first using it. Please try running

julia> ] build IntelVectorMath

If this does not work, please open an issue and include the output of <packagedir>/deps/build.log.

If you used this package prior to its renaming, you may have to run ] rm VML first. Otherwise, there will be a conflict due to the UUID.

After loading IntelVectorMath, you have the supported function listed below, for example IntelVectorMath.sin(rand(100)). These should provide a significant speed-up over broadcasting the Base functions. As the package name is quite long, the alias IVM is also exported to allow IVM.sin(rand(100)) after using the package. If you import the package, you can add this alias via const IVM = IntelVectorMath. Equally, you can replace IVM with another alias of your choice.

julia> using IntelVectorMath, BenchmarkTools

julia> a = randn(10^4);

julia> @btime sin.($a);     # apply Base.sin to each element
  102.128 μs (2 allocations: 78.20 KiB)

julia> @btime IVM.sin($a);  # apply IVM.sin to the whole array
  20.900 μs (2 allocations: 78.20 KiB)

julia> b = similar(a);

julia> @btime IVM.sin!(b, a);  # in-place version
  20.008 μs (0 allocations: 0 bytes)

julia> @views IVM.sin(a[1:2:end]) == b[1:2:end] # all IVM functions support 1d strided input
true

By default, IntelVectorMath uses VML_HA mode, which corresponds to an accuracy of <1 ulp, matching the accuracy of Julia's built-in openlibm implementation, although the exact results may be different. To specify low accuracy, use vml_set_accuracy(VML_LA). To specify enhanced performance, use vml_set_accuracy(VML_EP). More documentation regarding these options is available on Intel's website.

On some CPU, operations on denormalized numbers are extremely slow. You case use vml_set_denormalmode(VML_DENORMAL_FAST) to handle denormalized numbers as zero. See the ?VML_DENORMAL_FAST for more information. You can get the current mode by vml_get_denormalmode(). The default is VML_DENORMAL_ACCURATE.

By default, IntelVectorMath uses multithreading. The maximum number of threads that a call may use is given by vml_get_max_threads(). On most environment this will default to the number of physical cores available to IntelVectorMath. This behavior can be changed using vml_set_num_threads(numthreads).

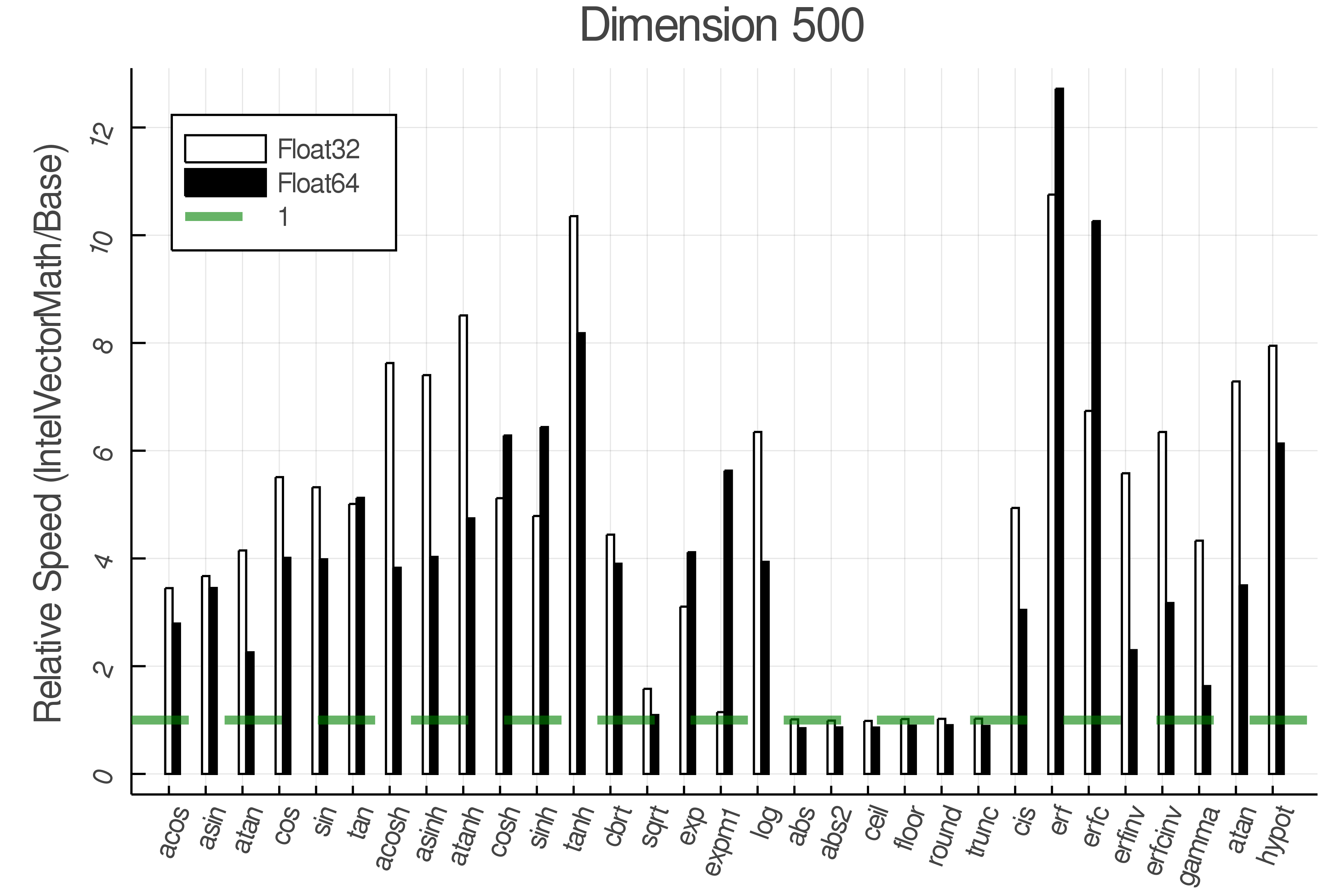
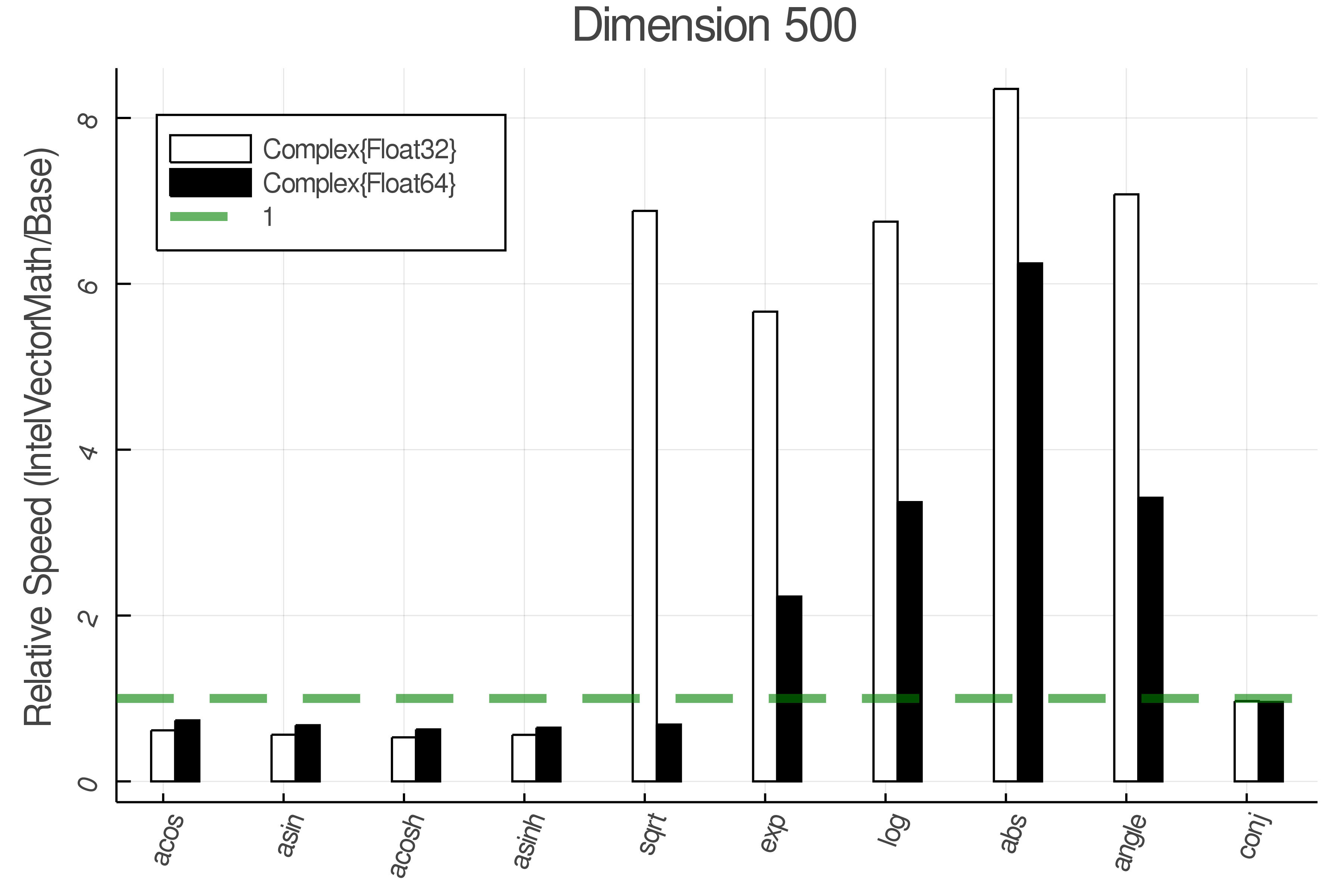
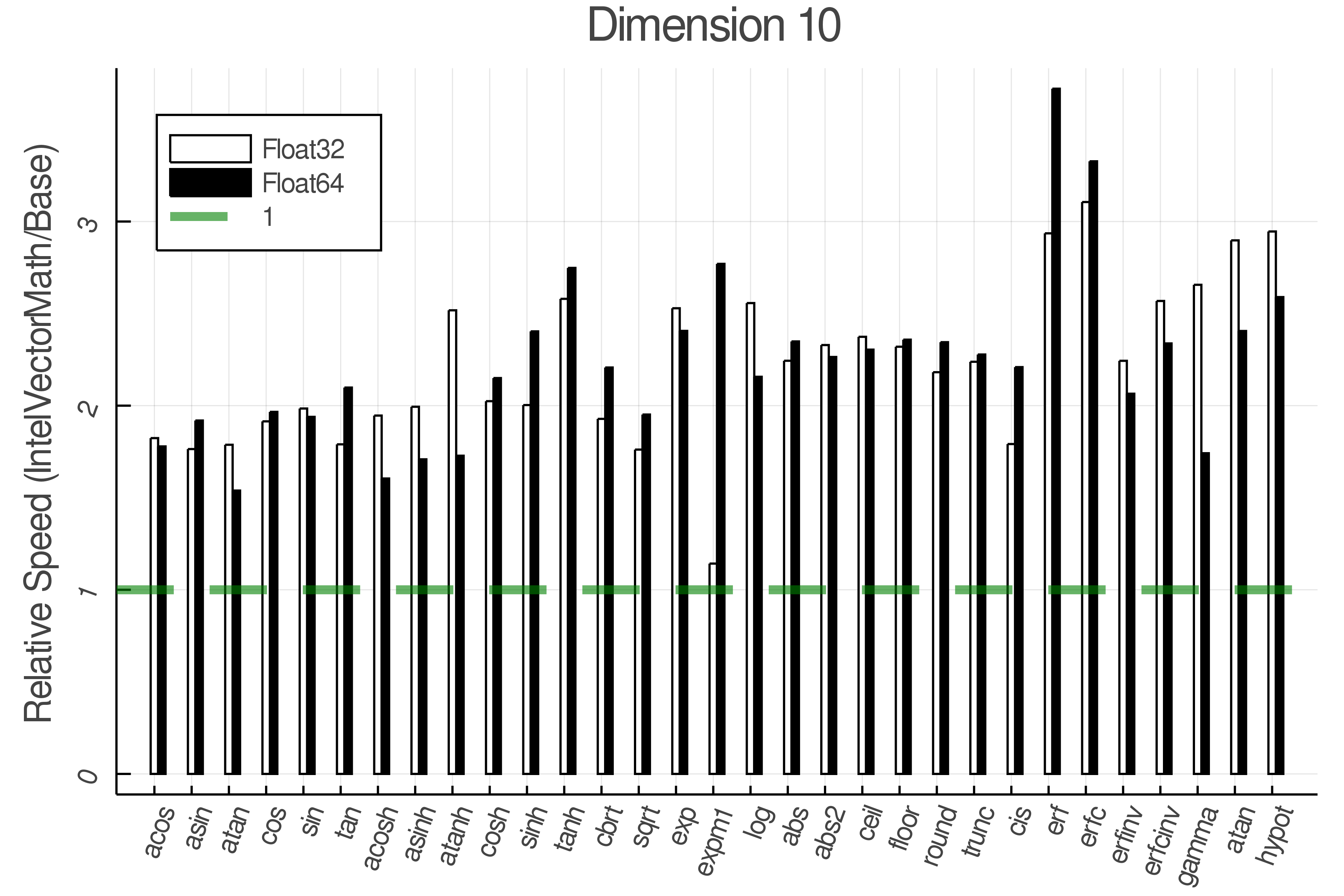
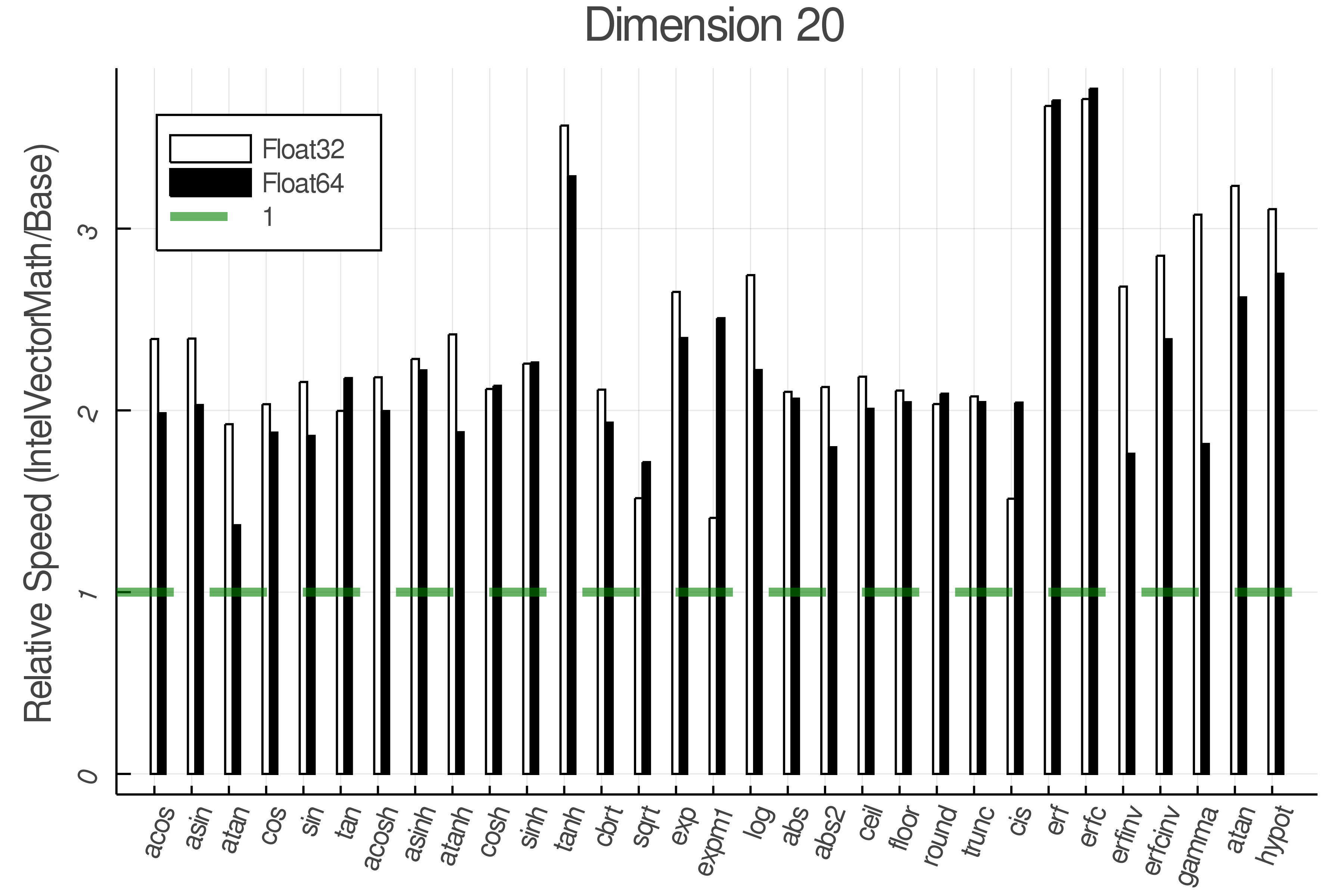
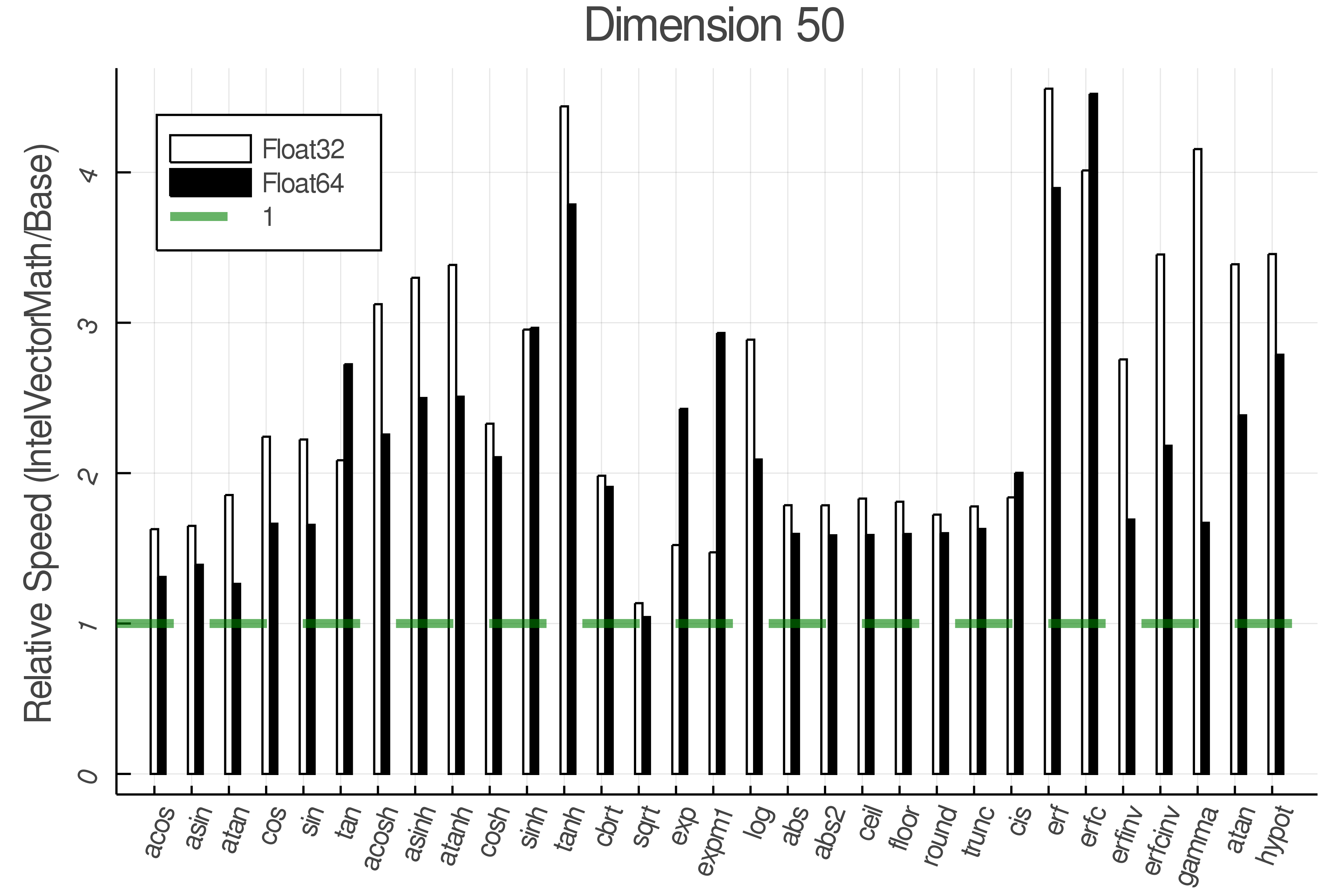
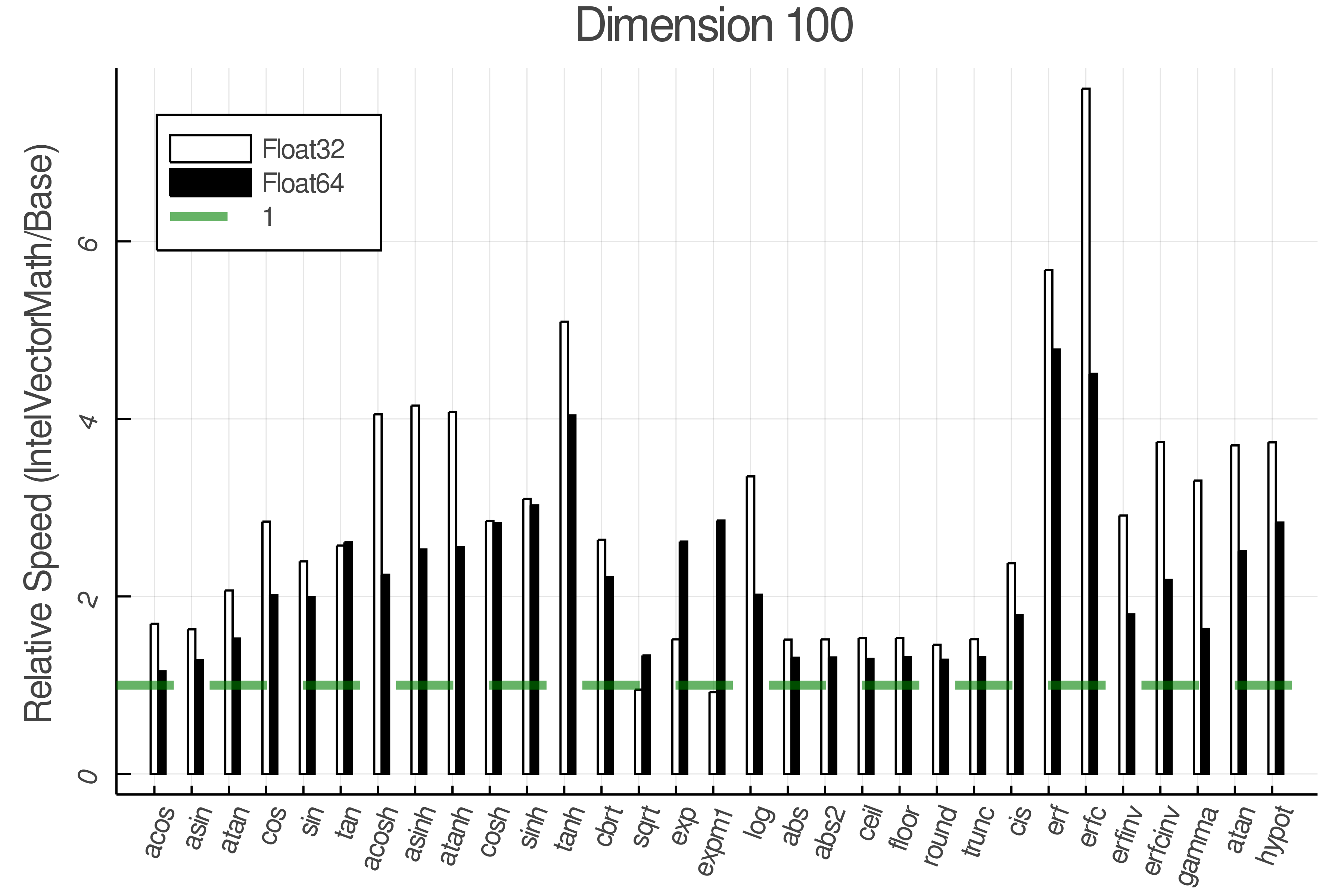
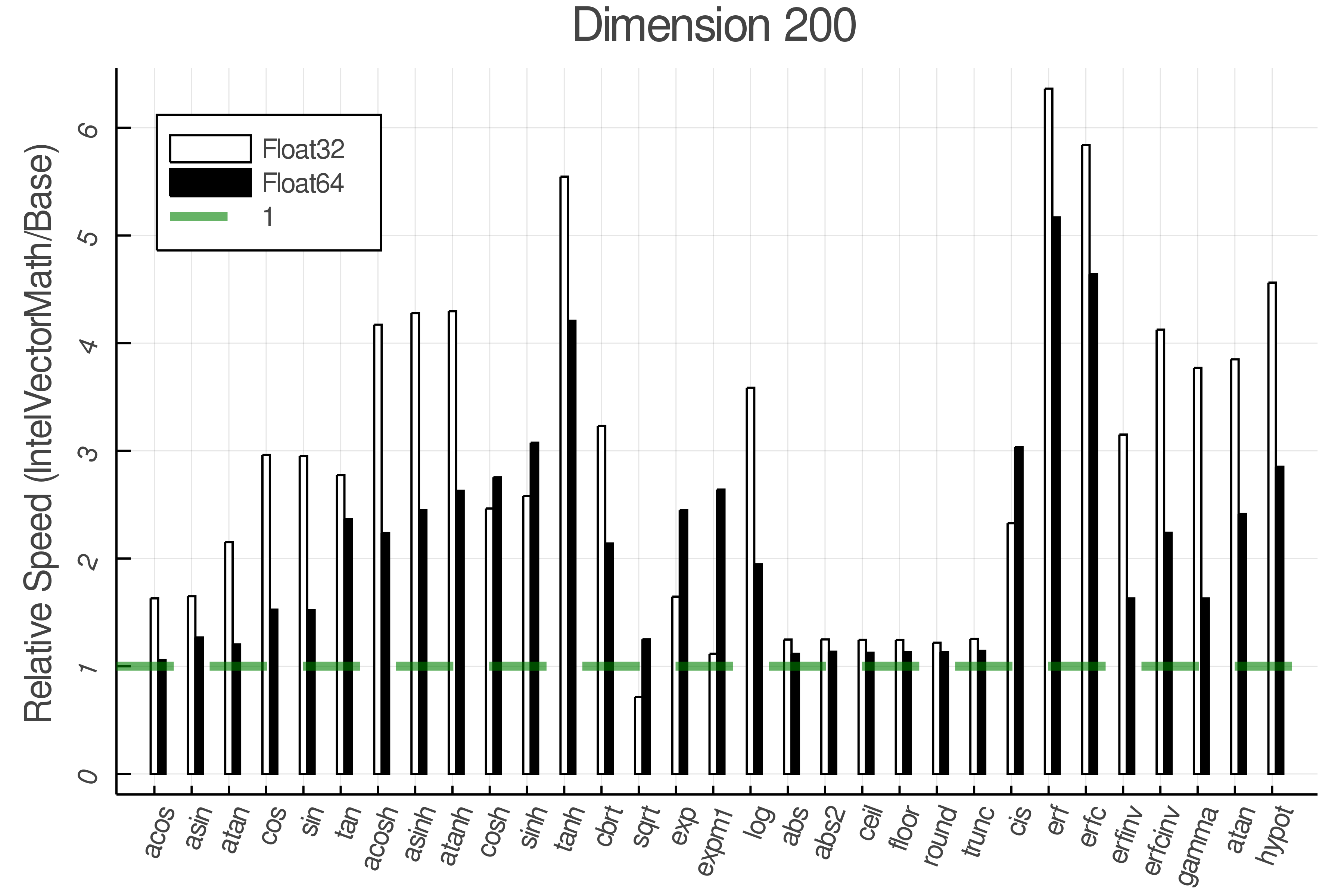
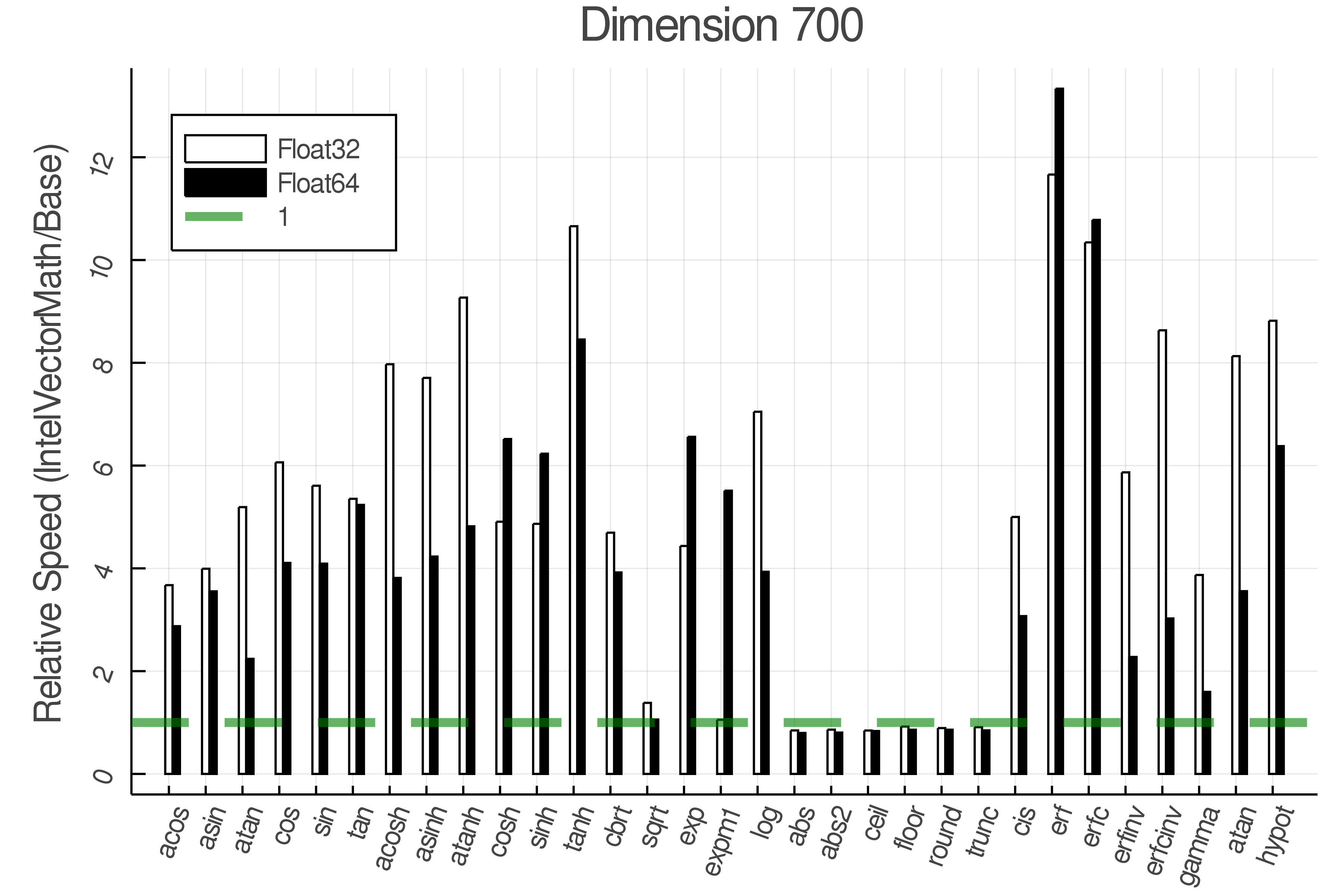
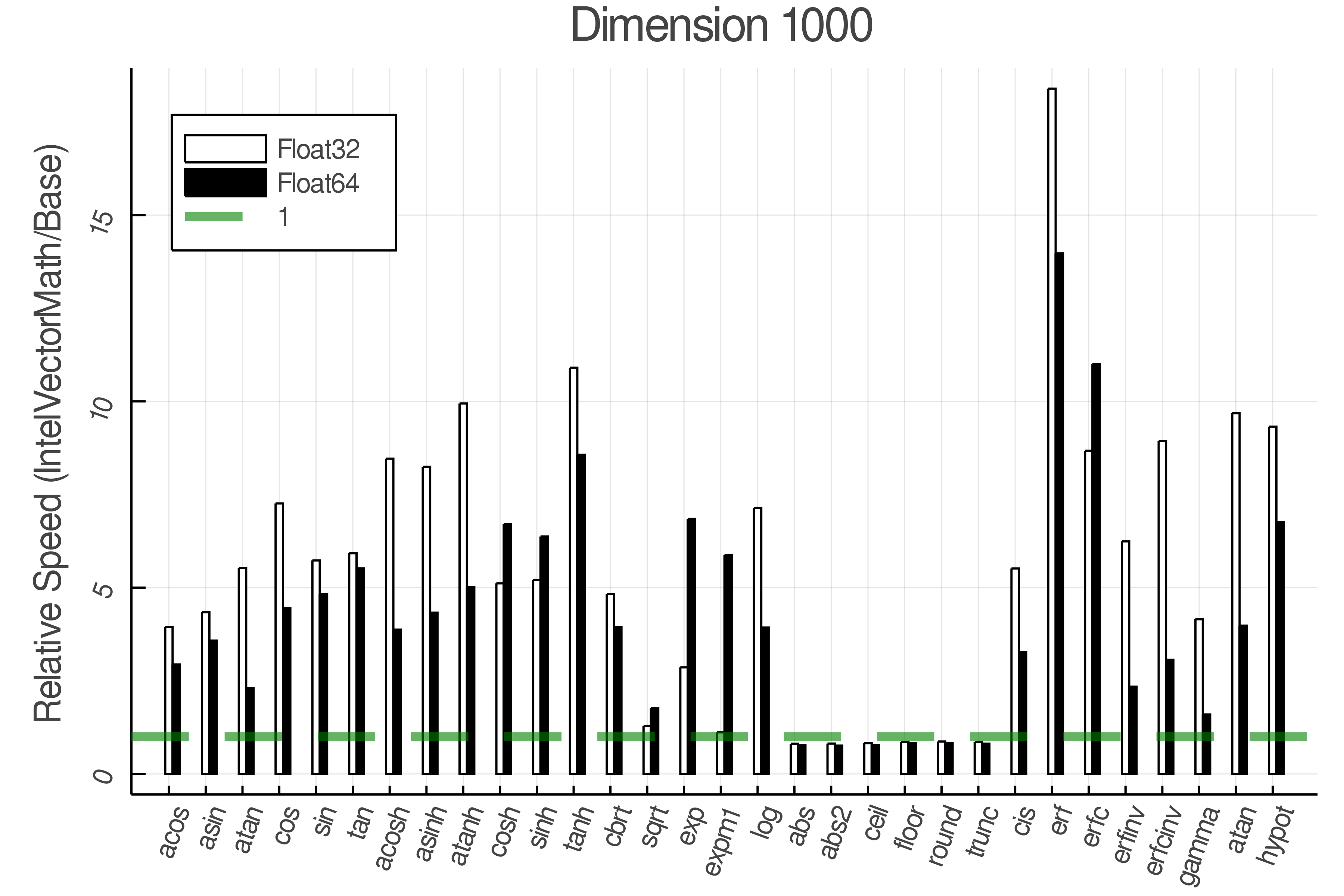
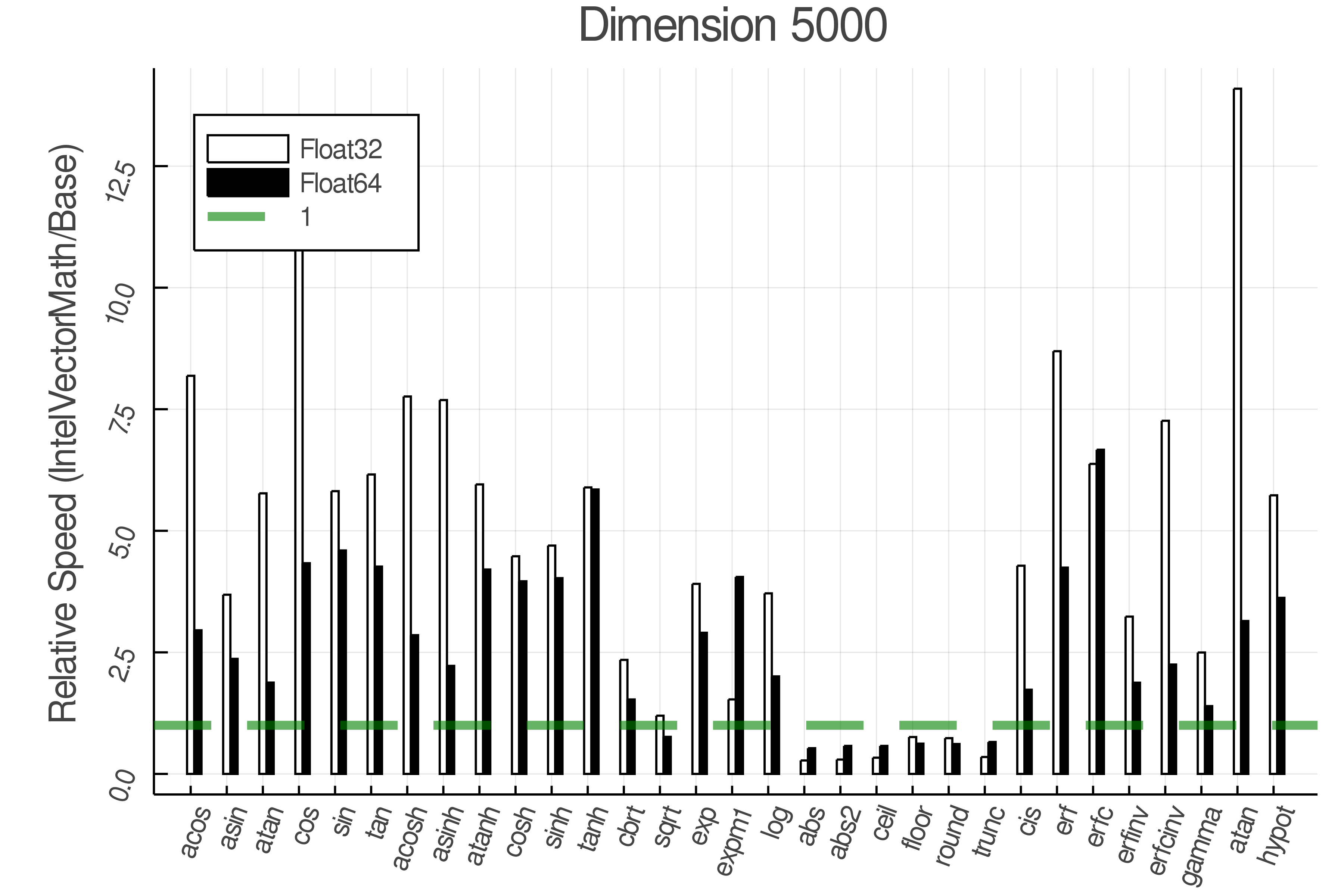
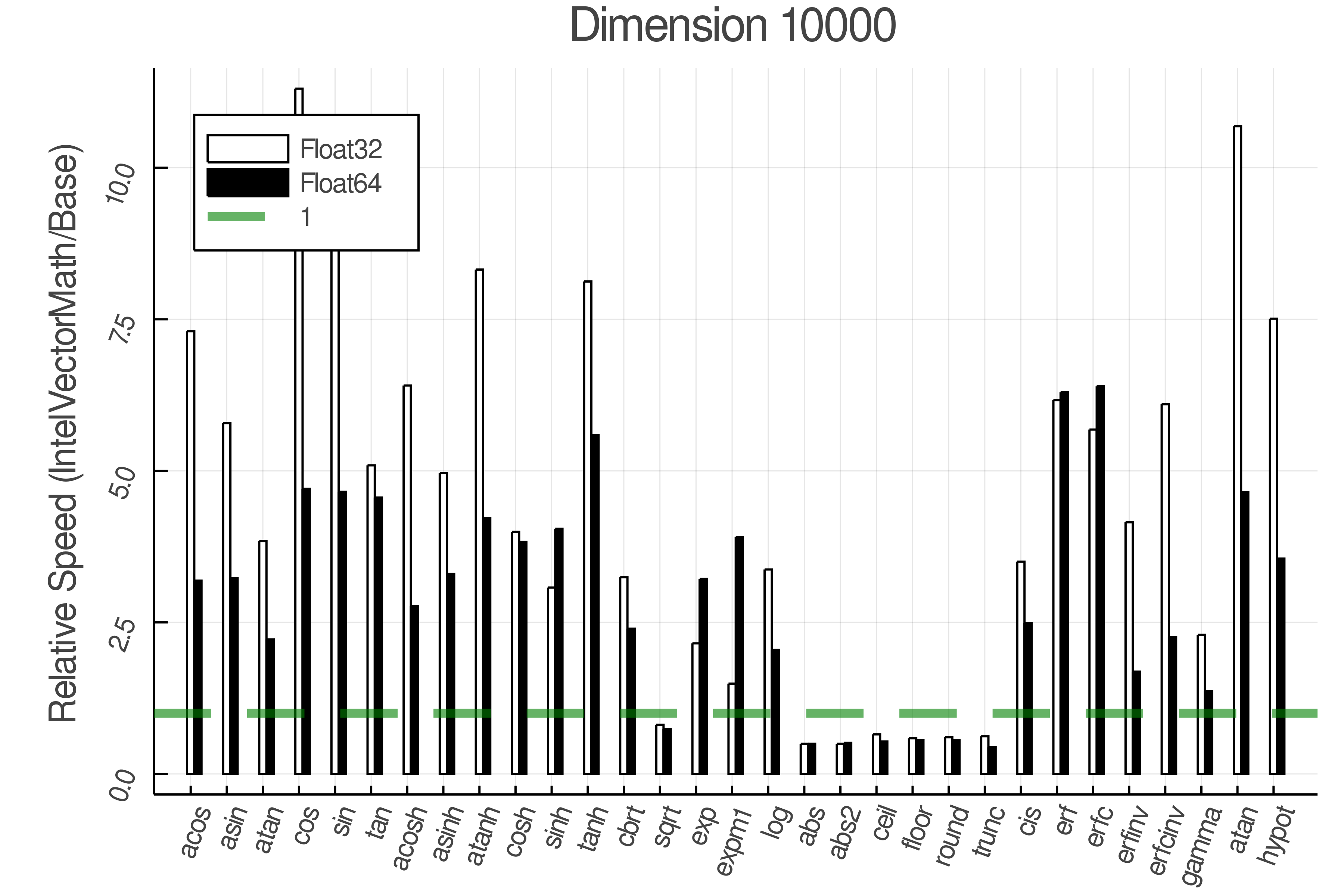
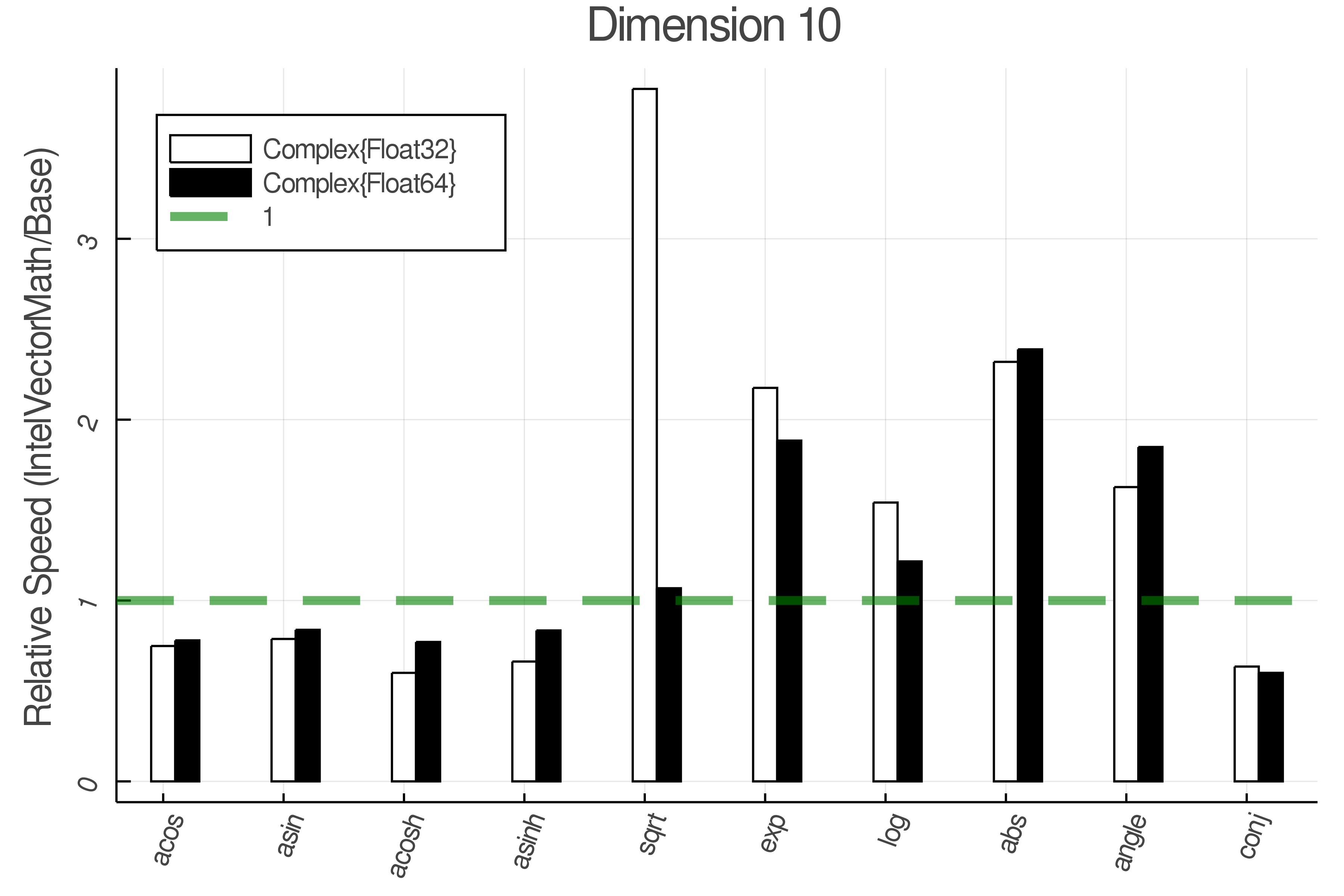
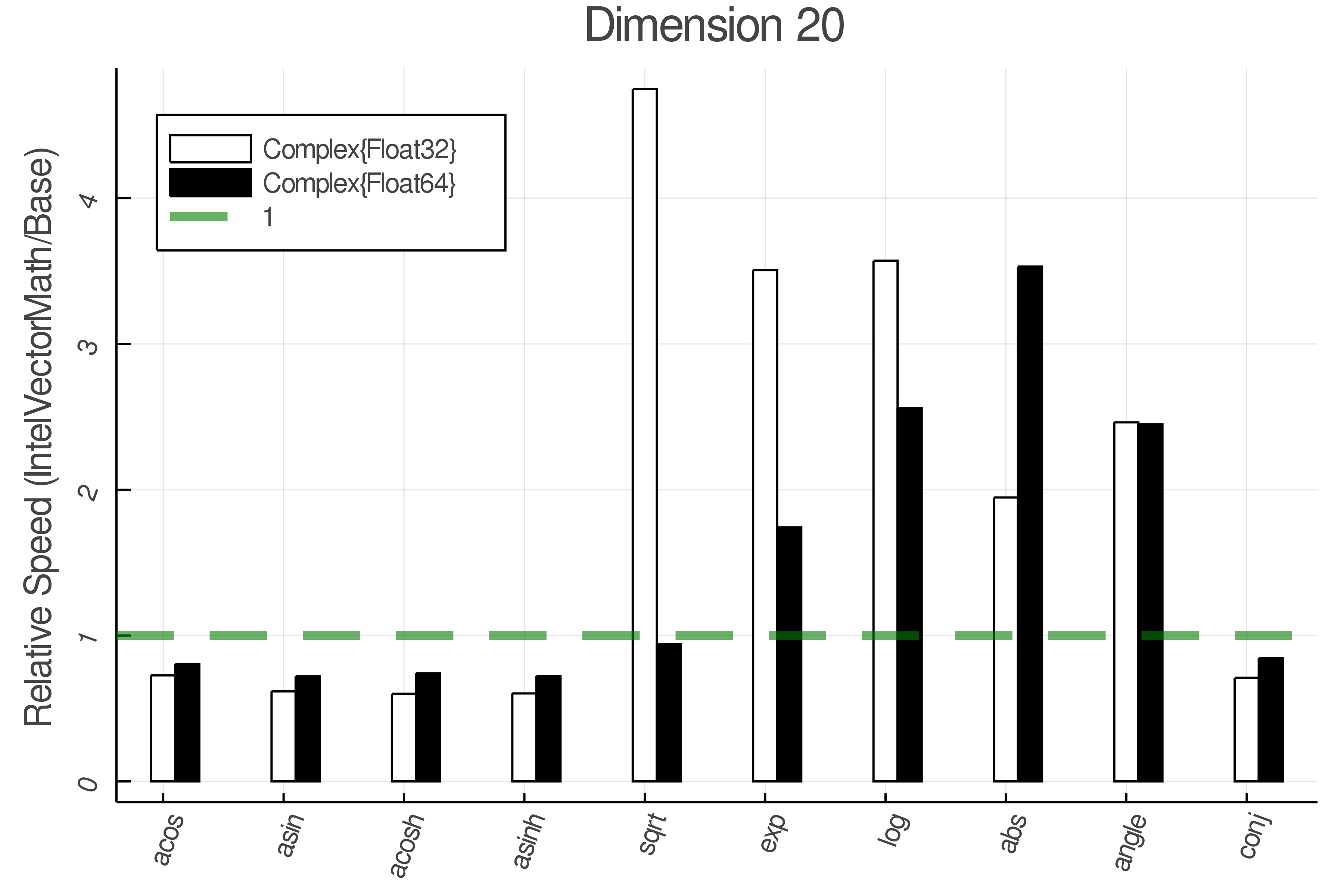
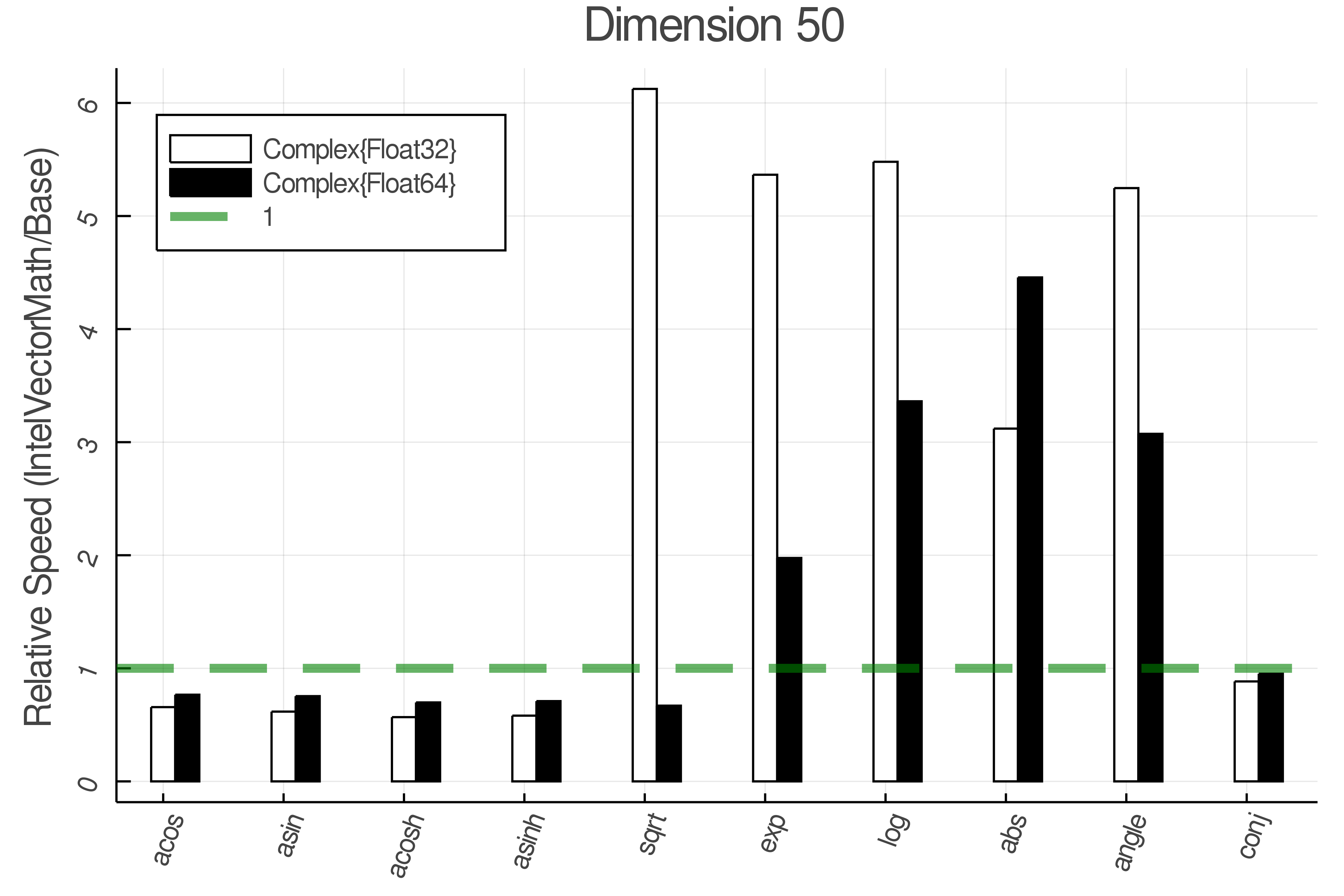
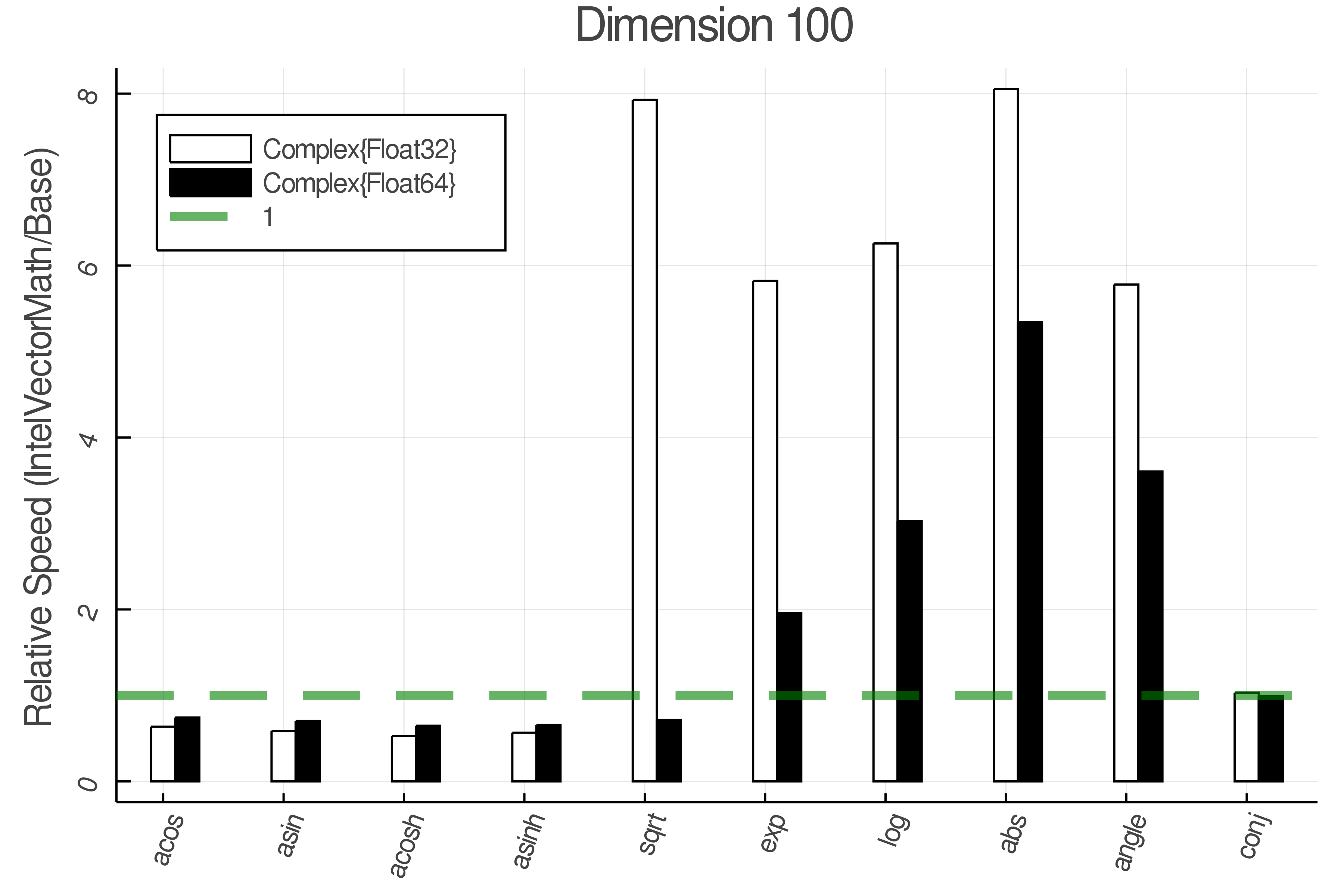
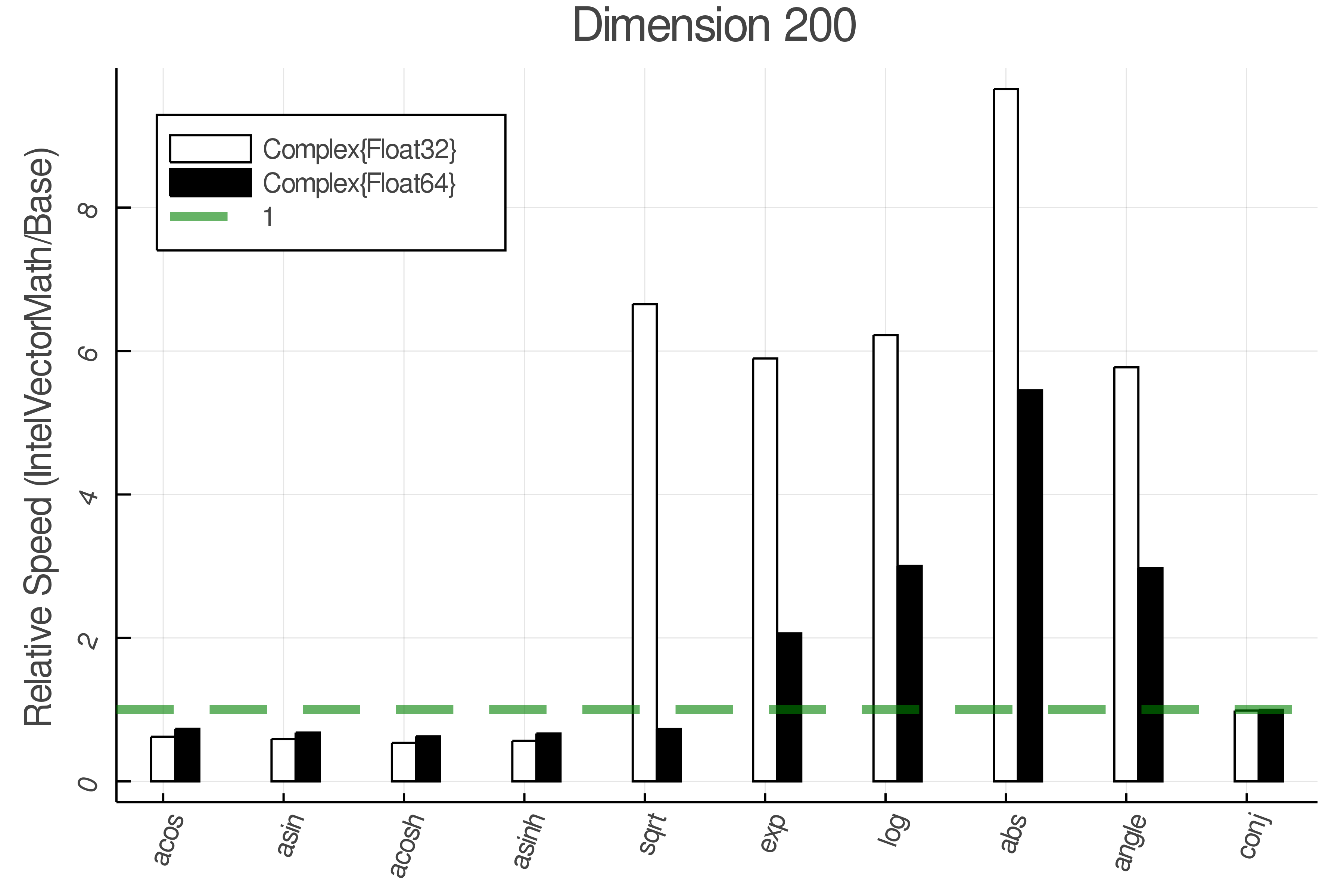
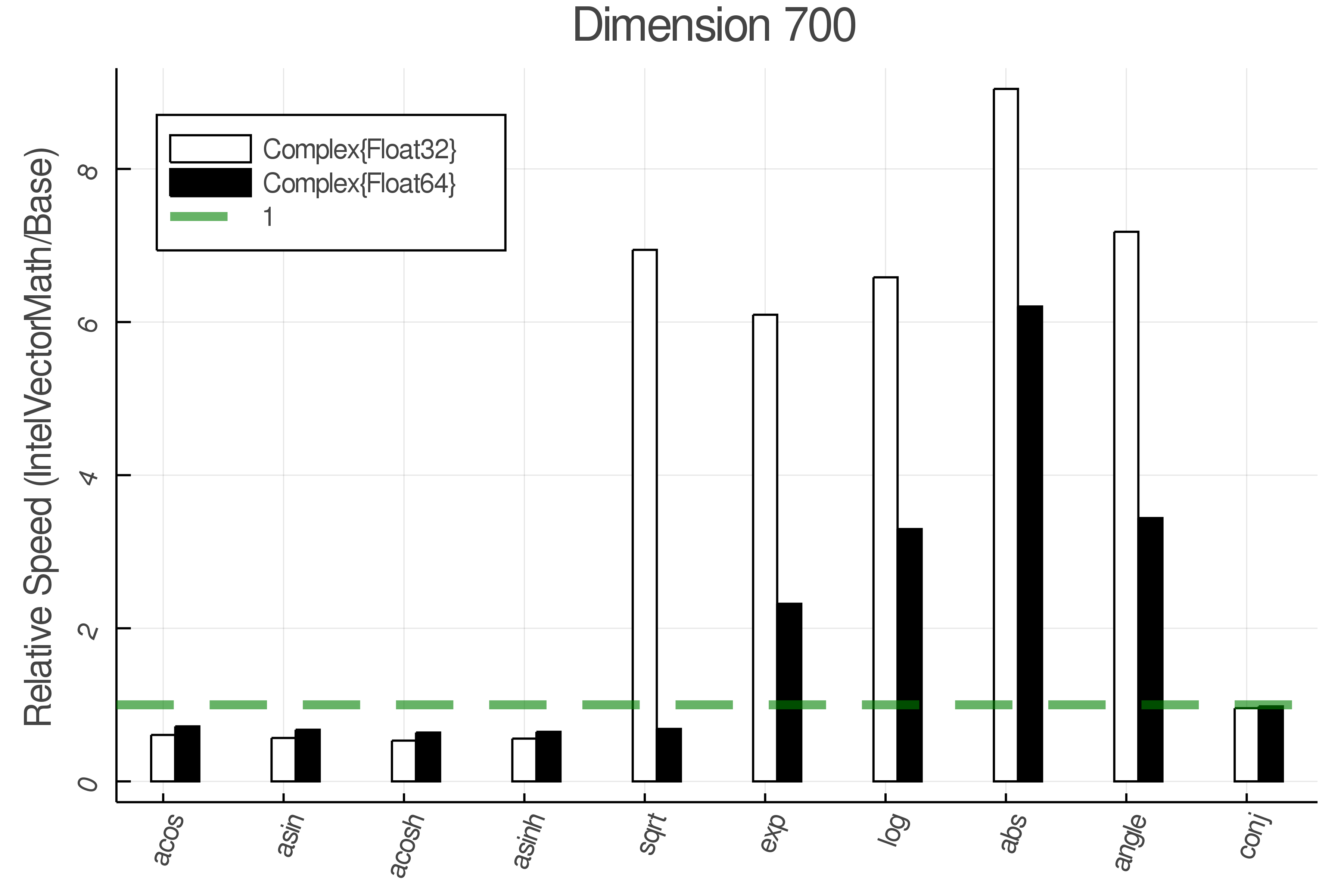
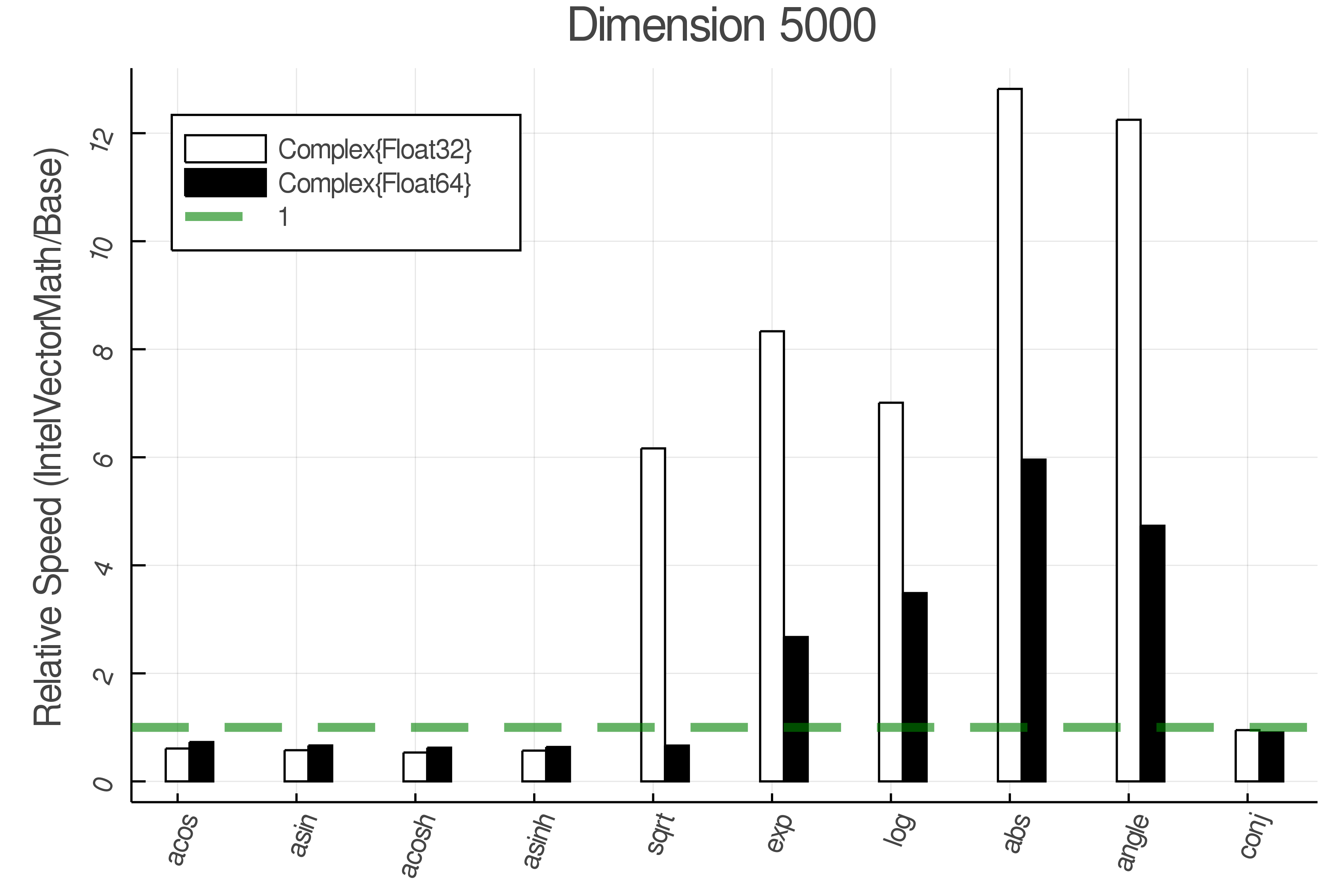
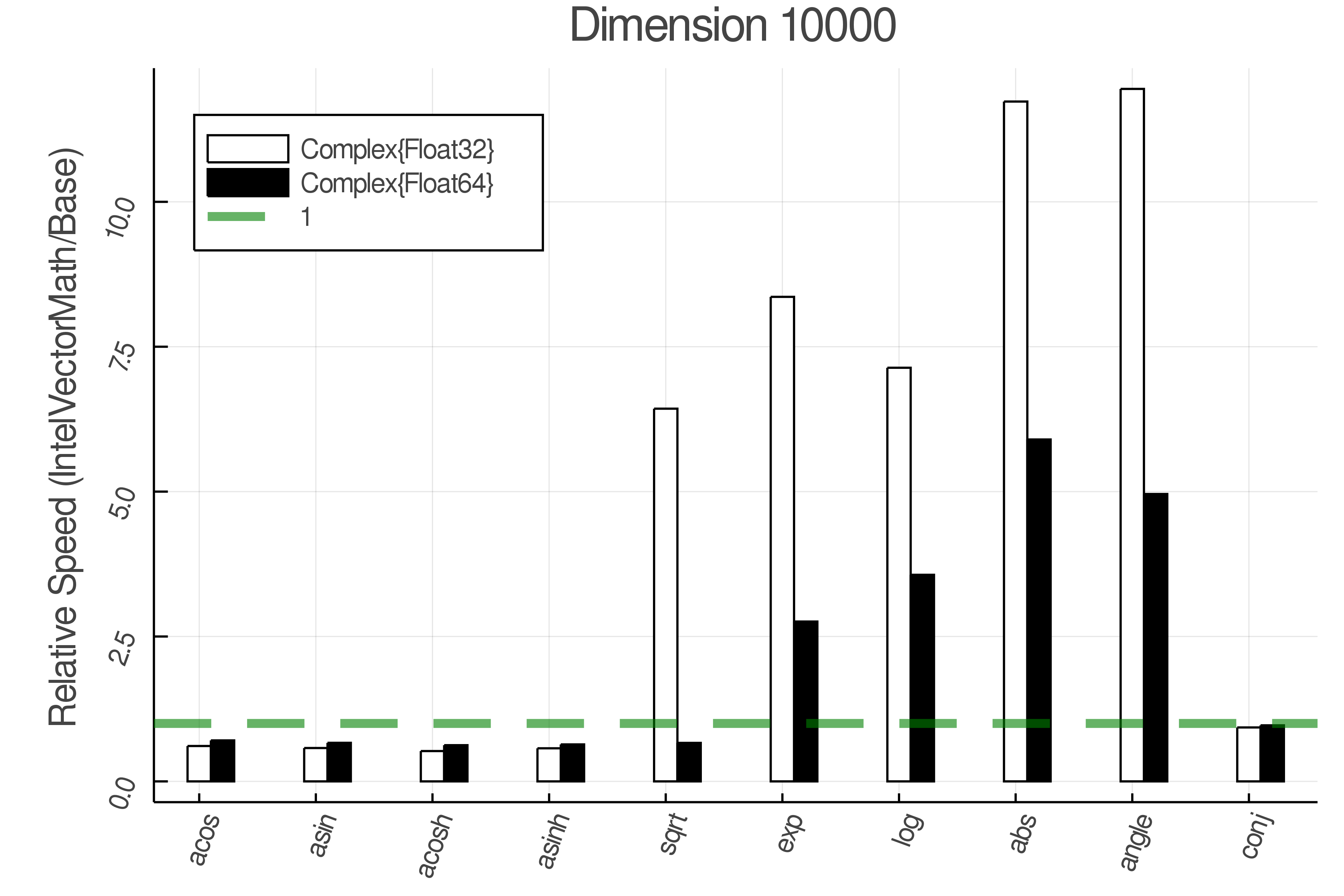
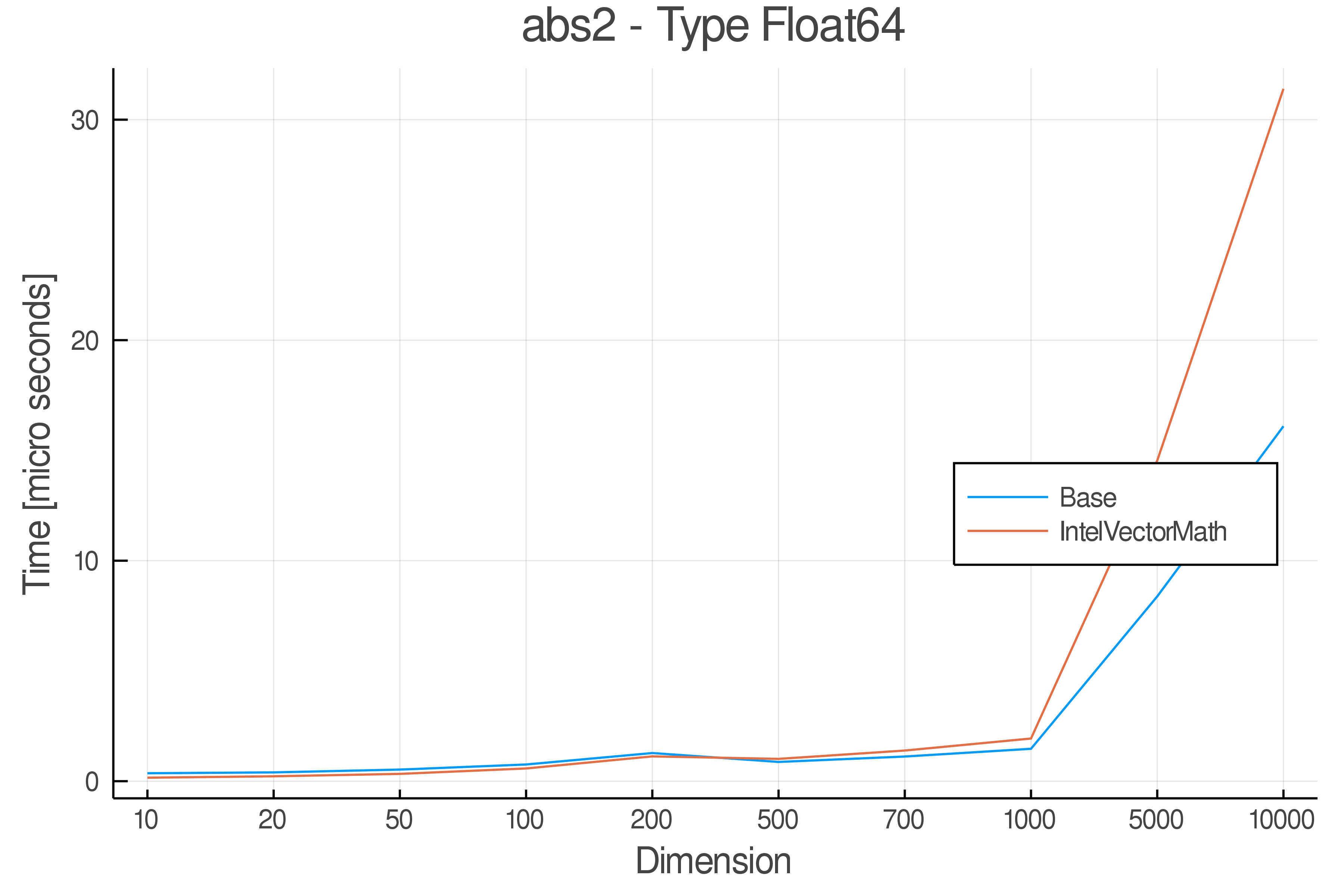
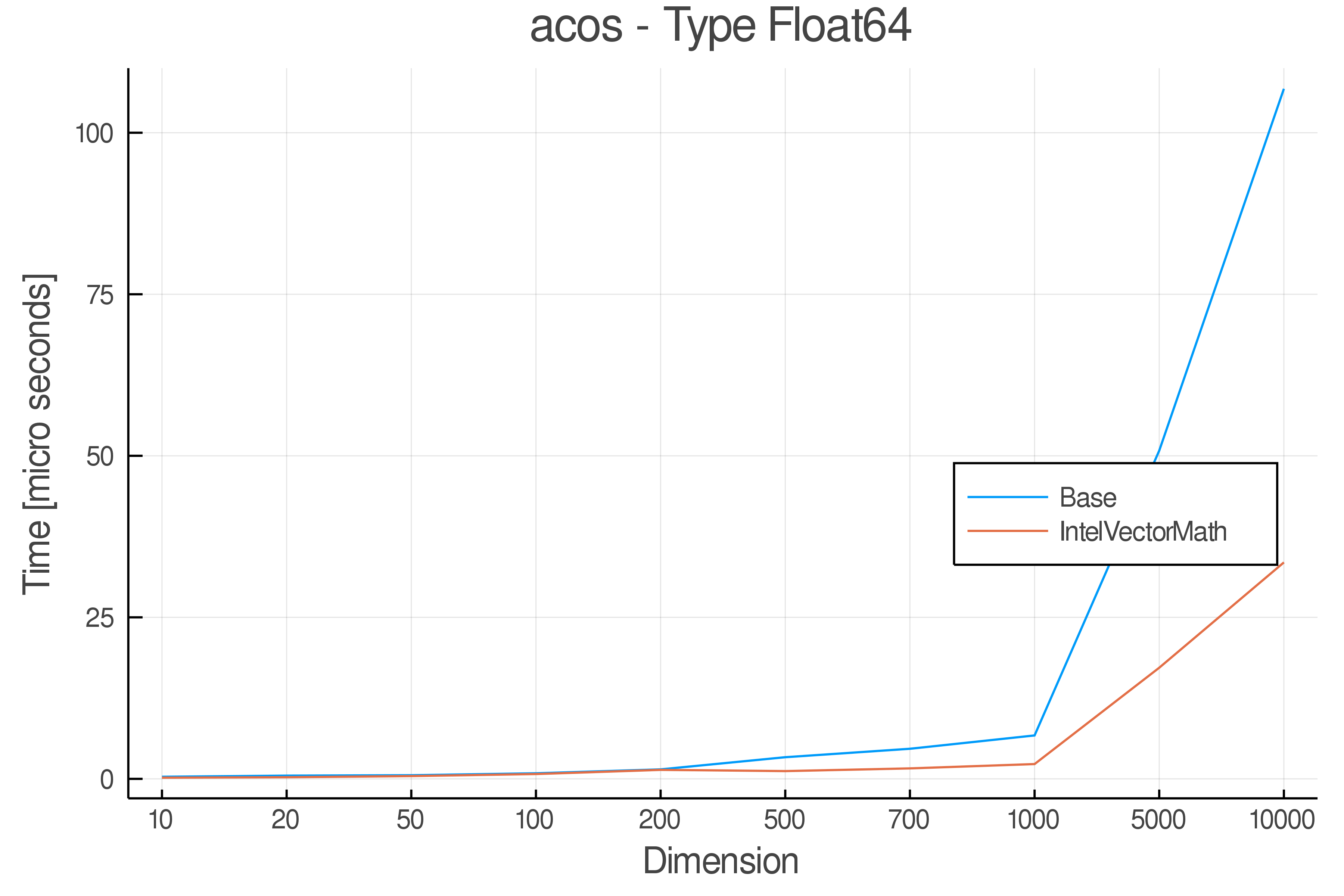
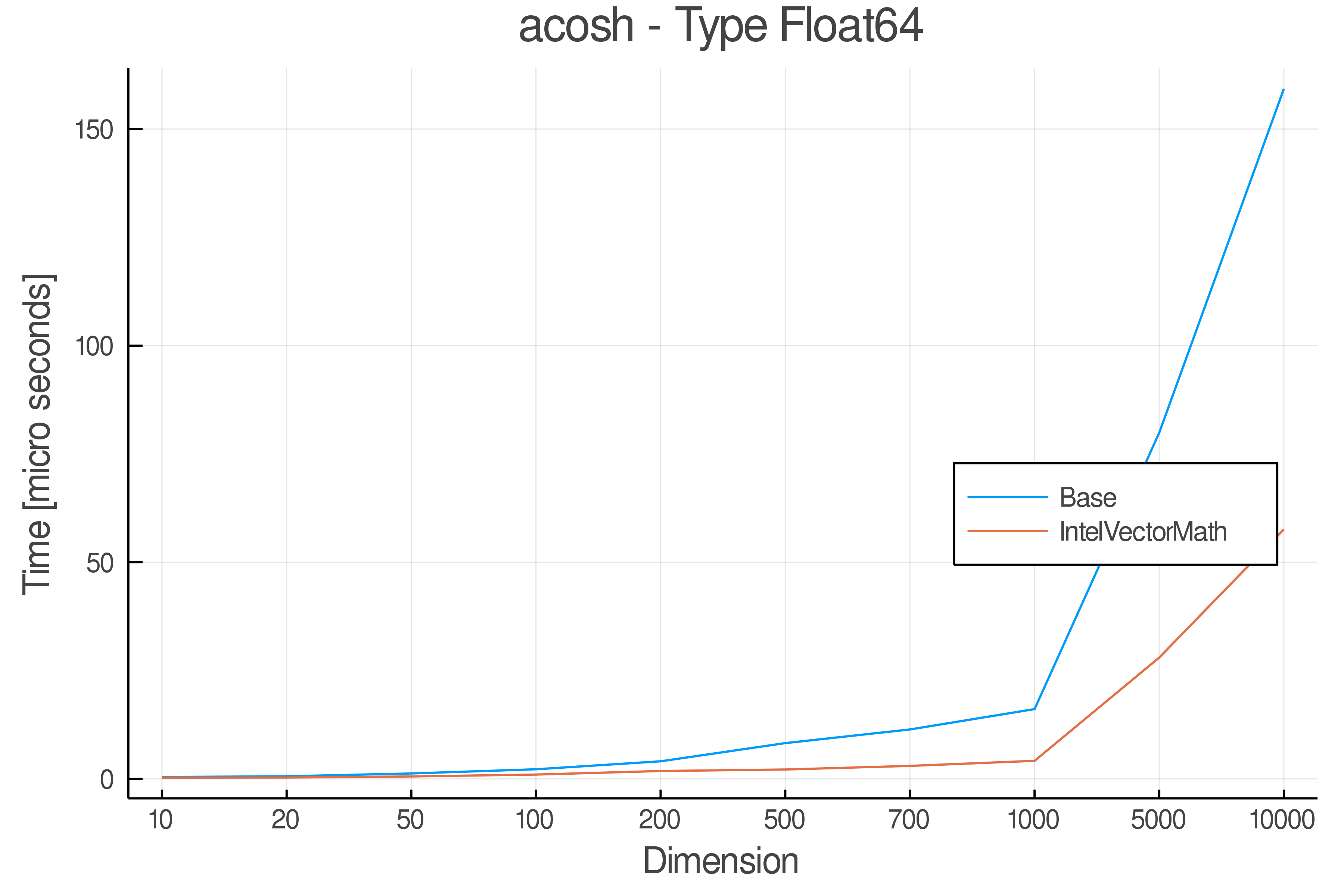
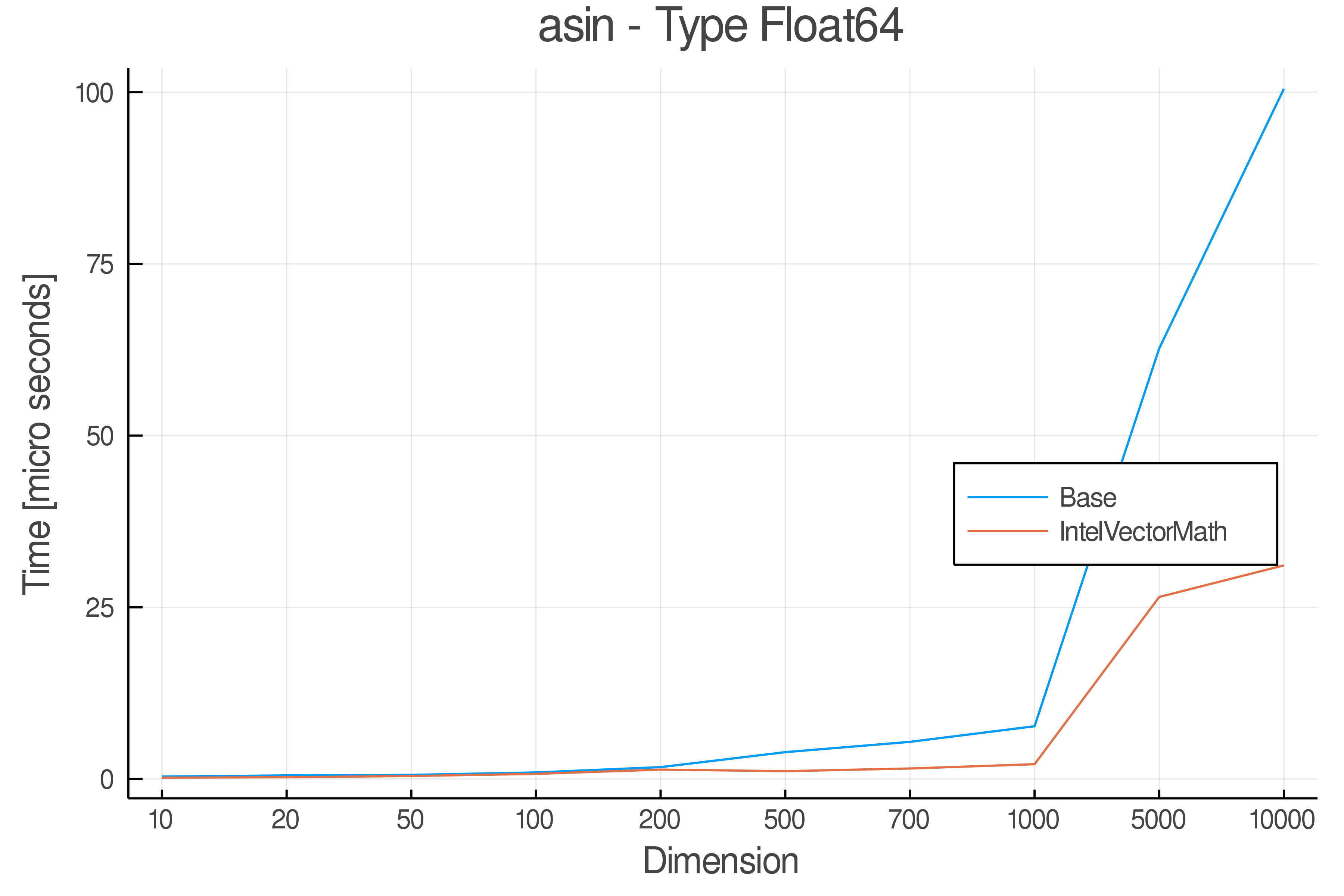
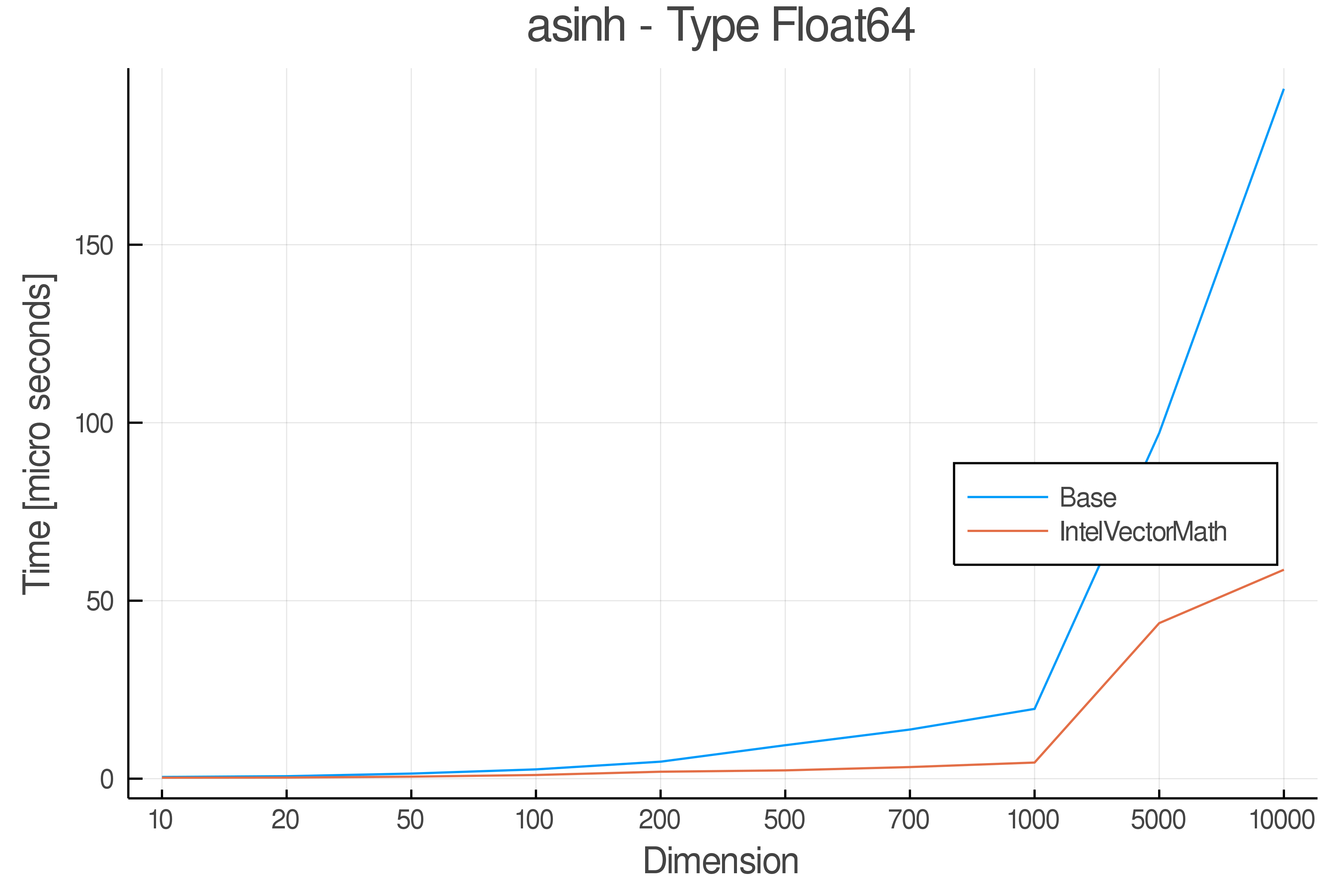
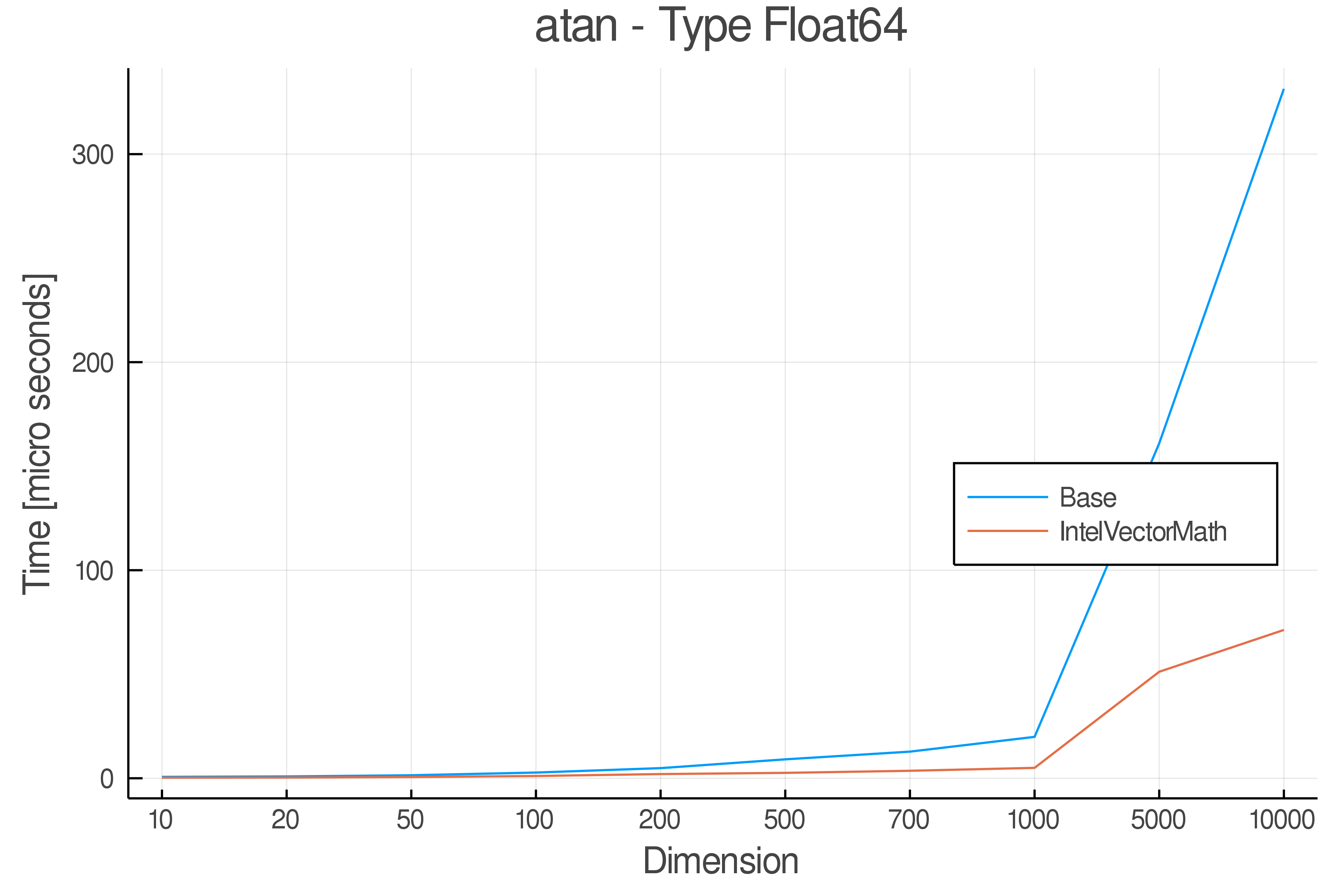
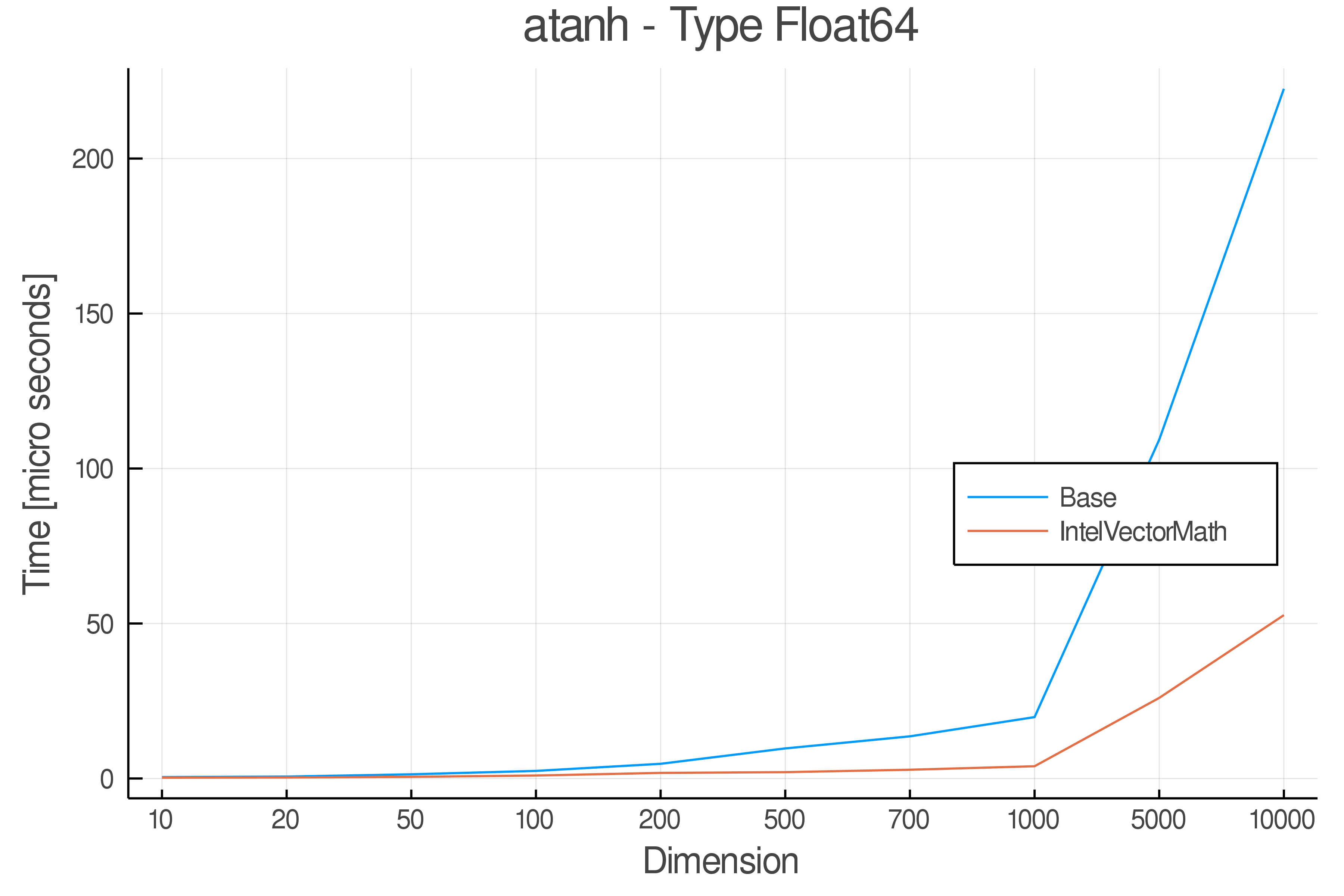
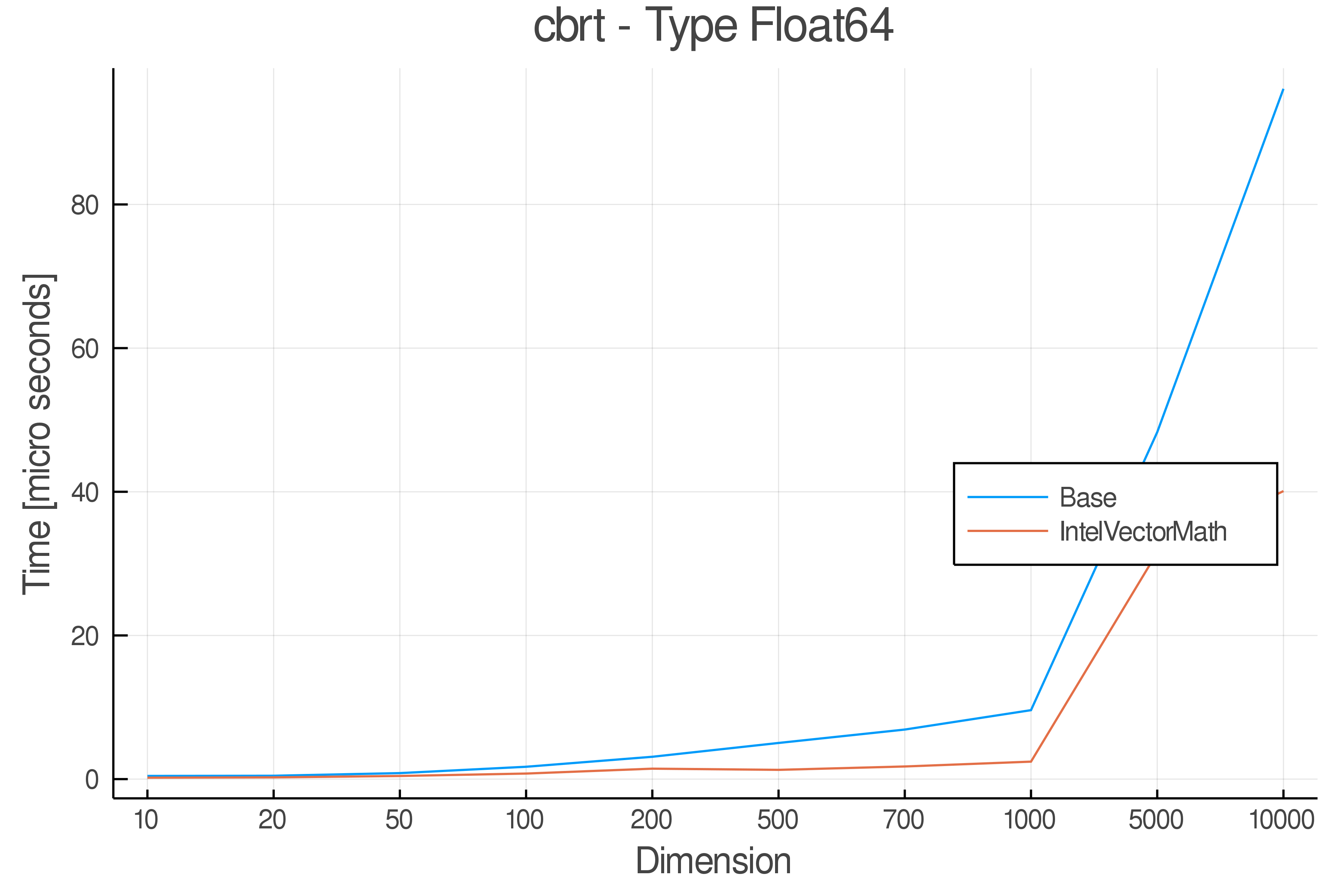
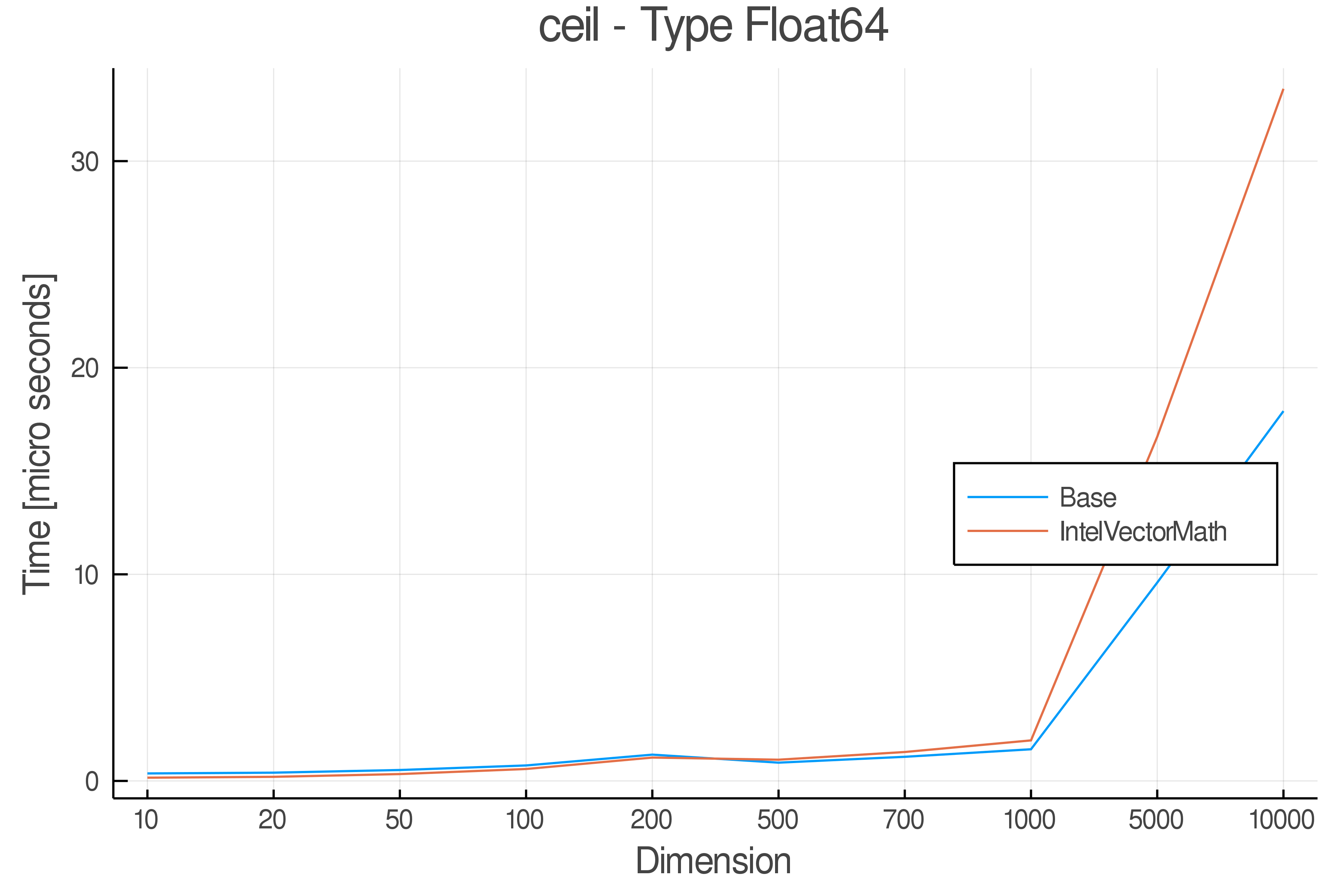
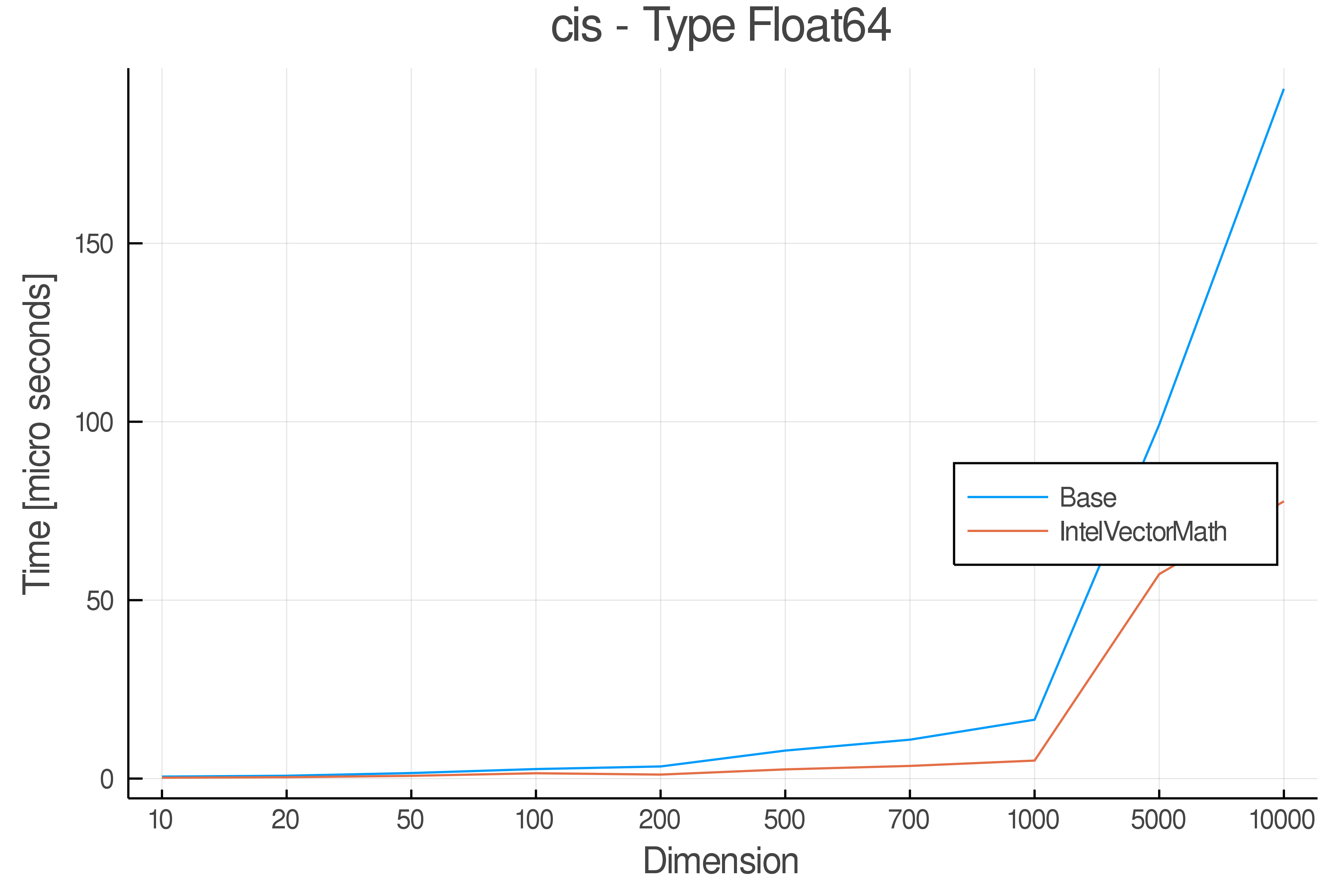
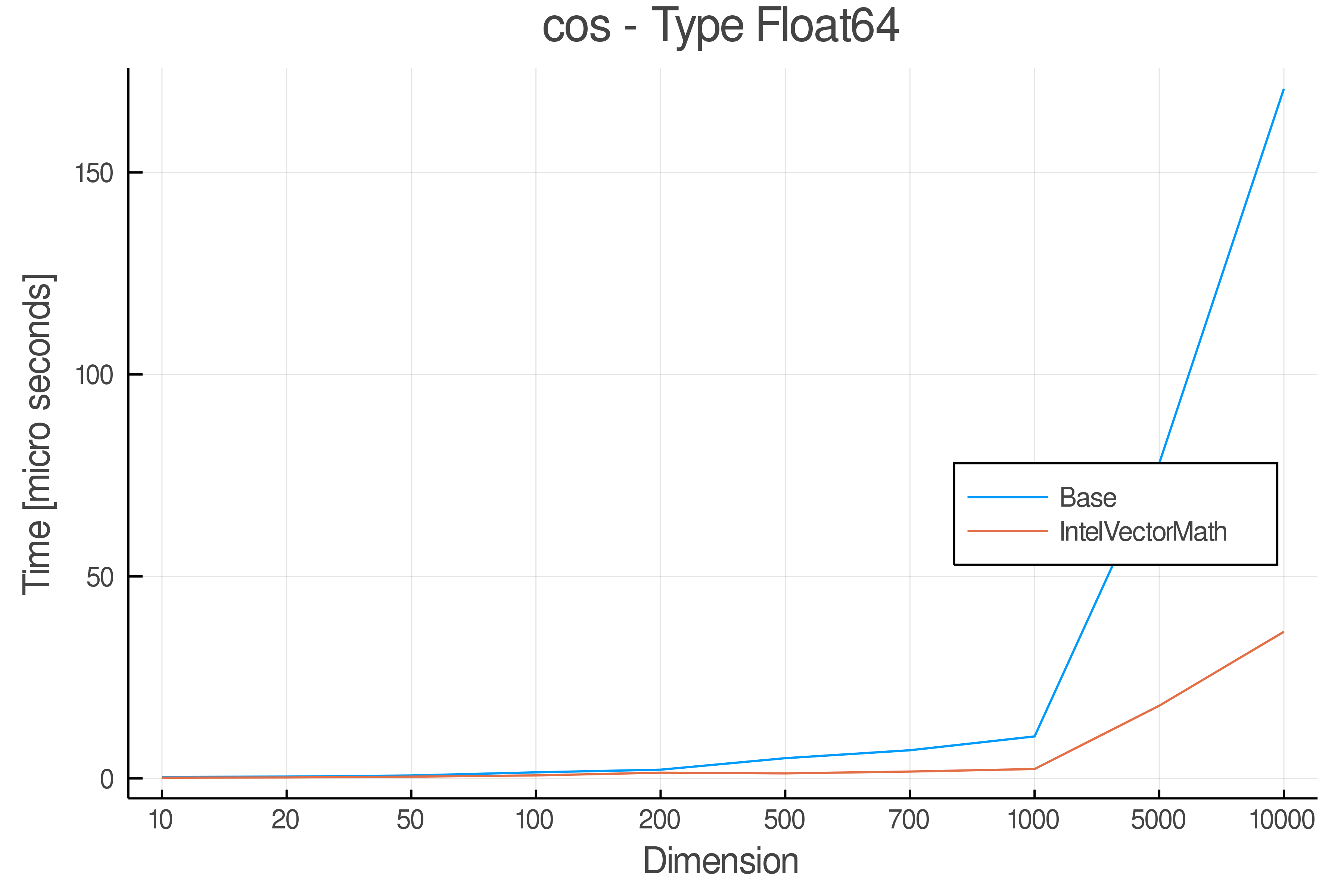
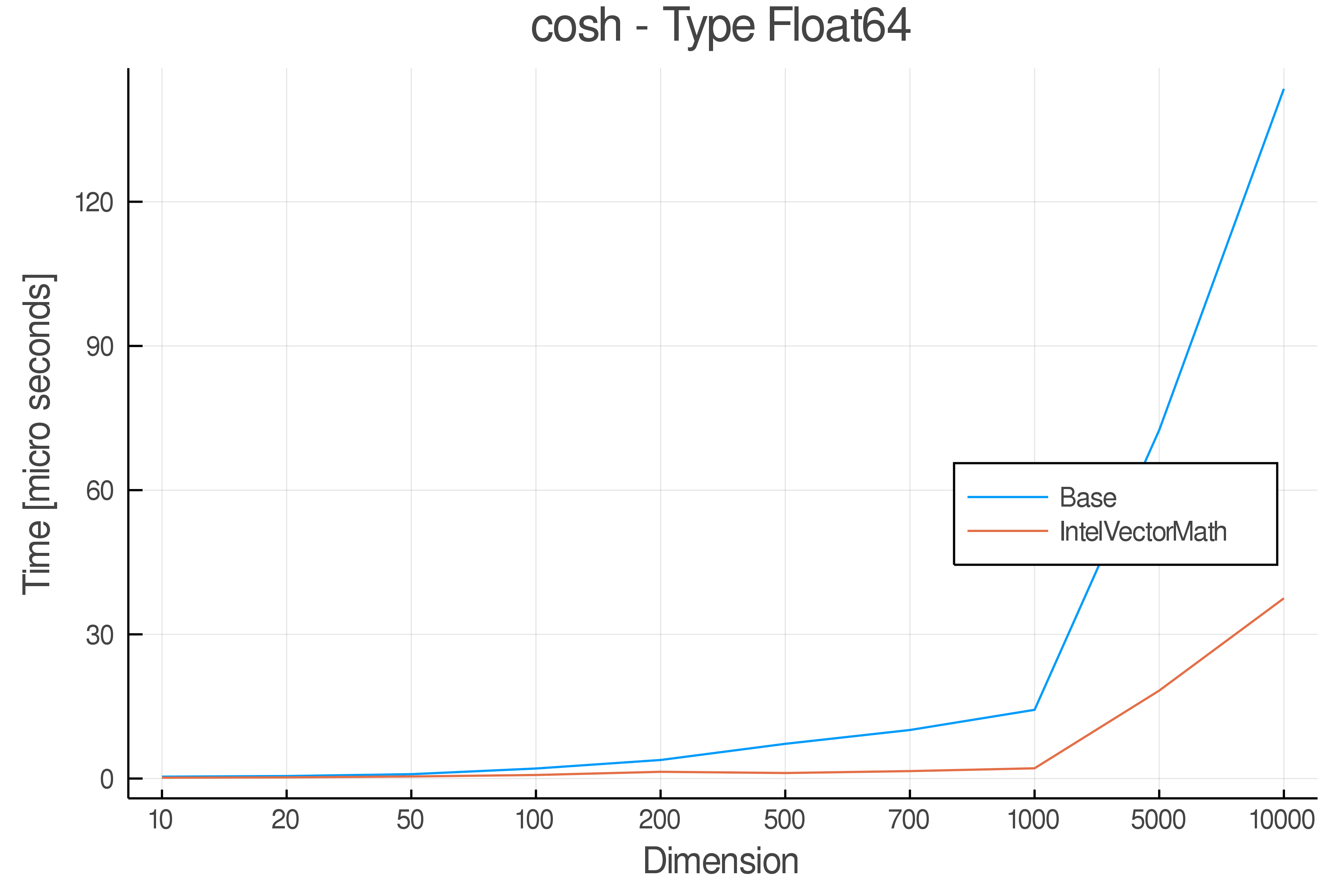
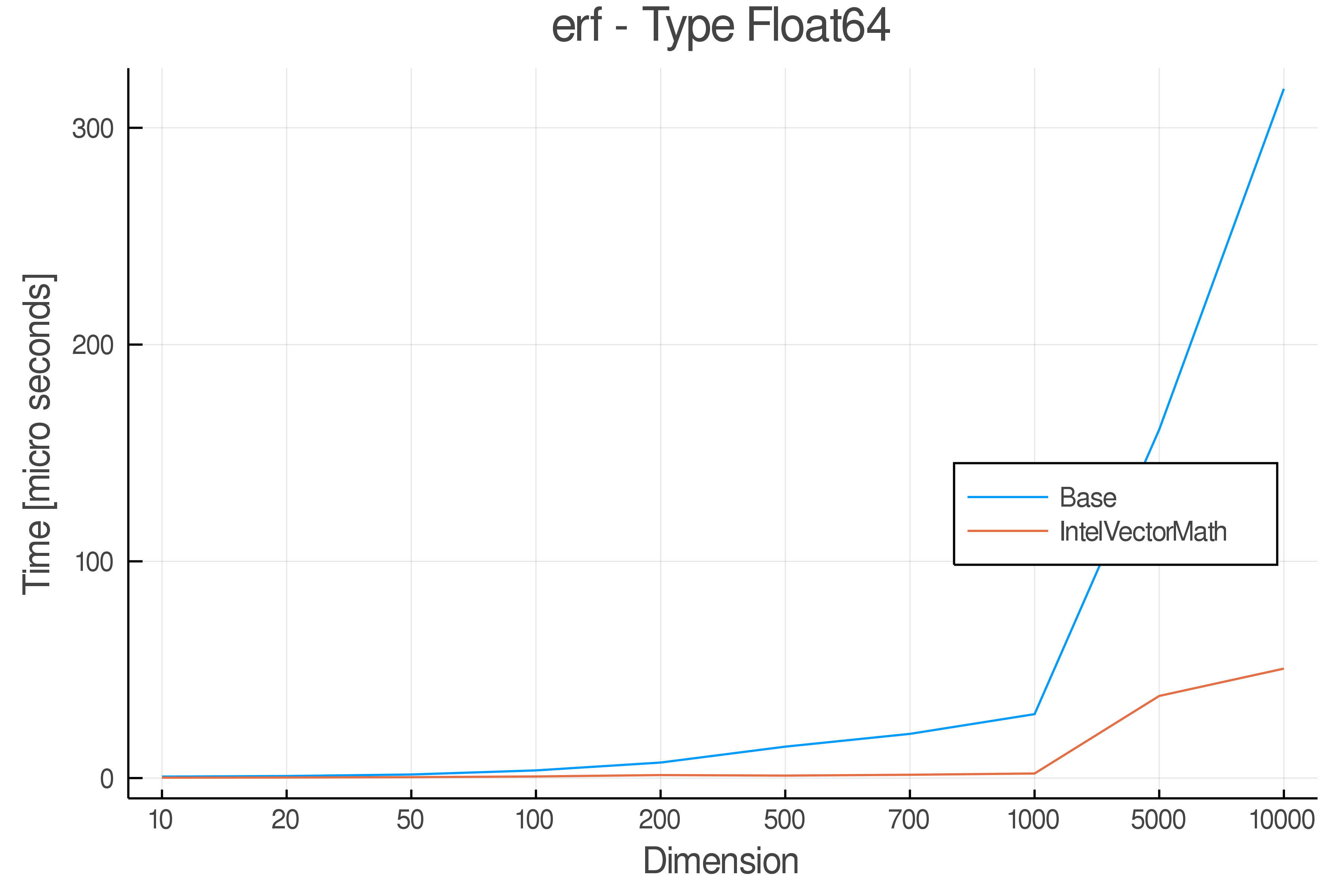
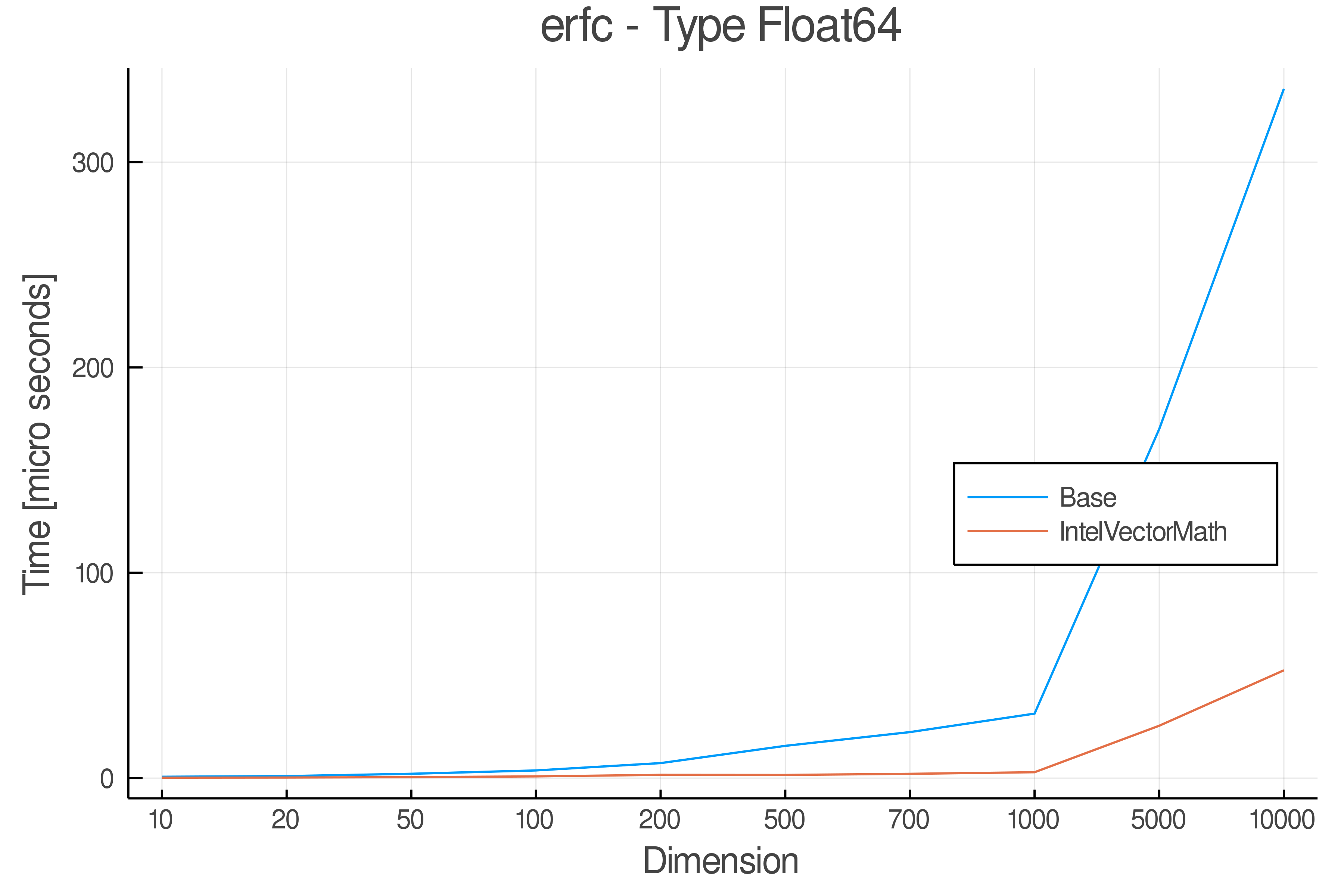
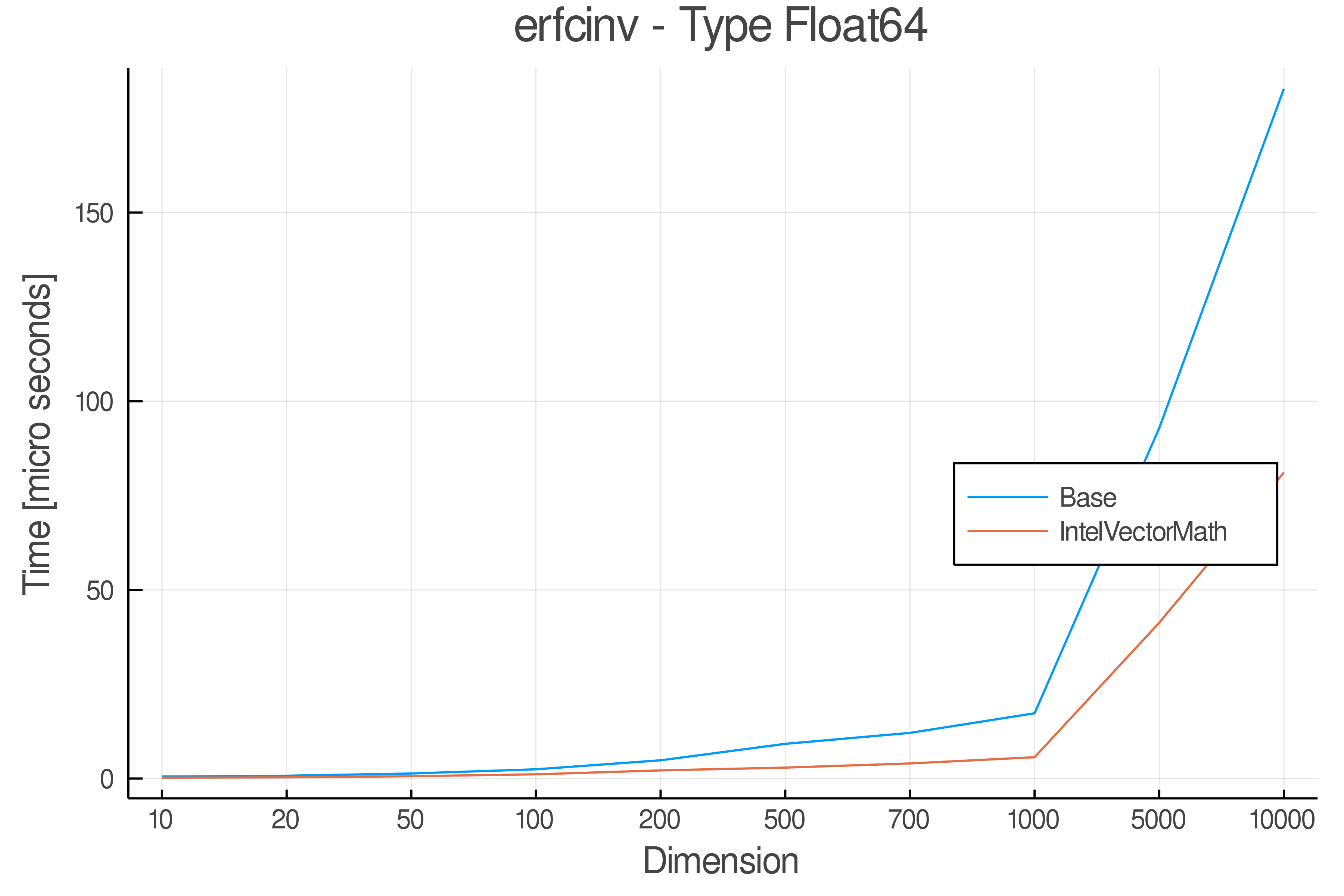
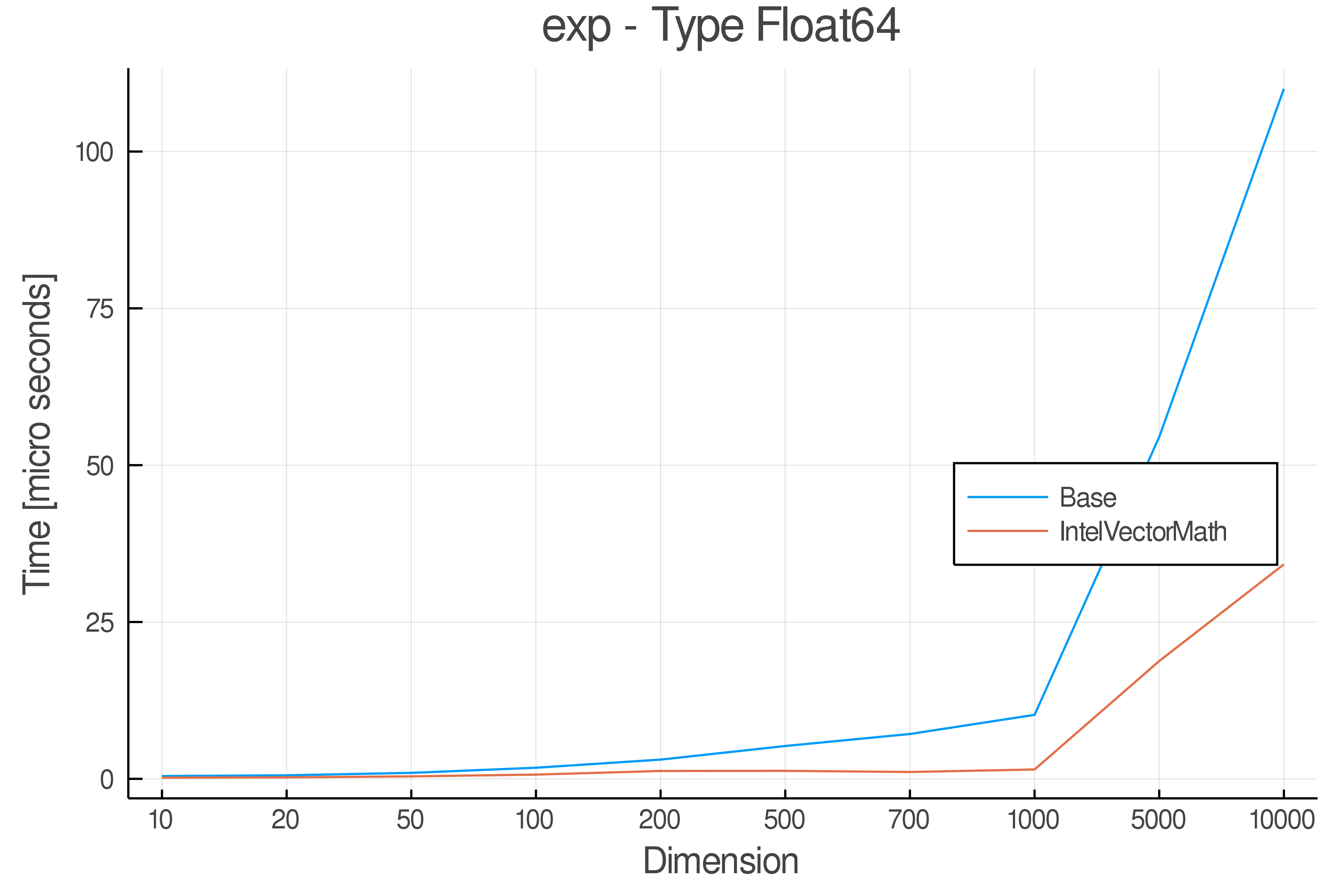
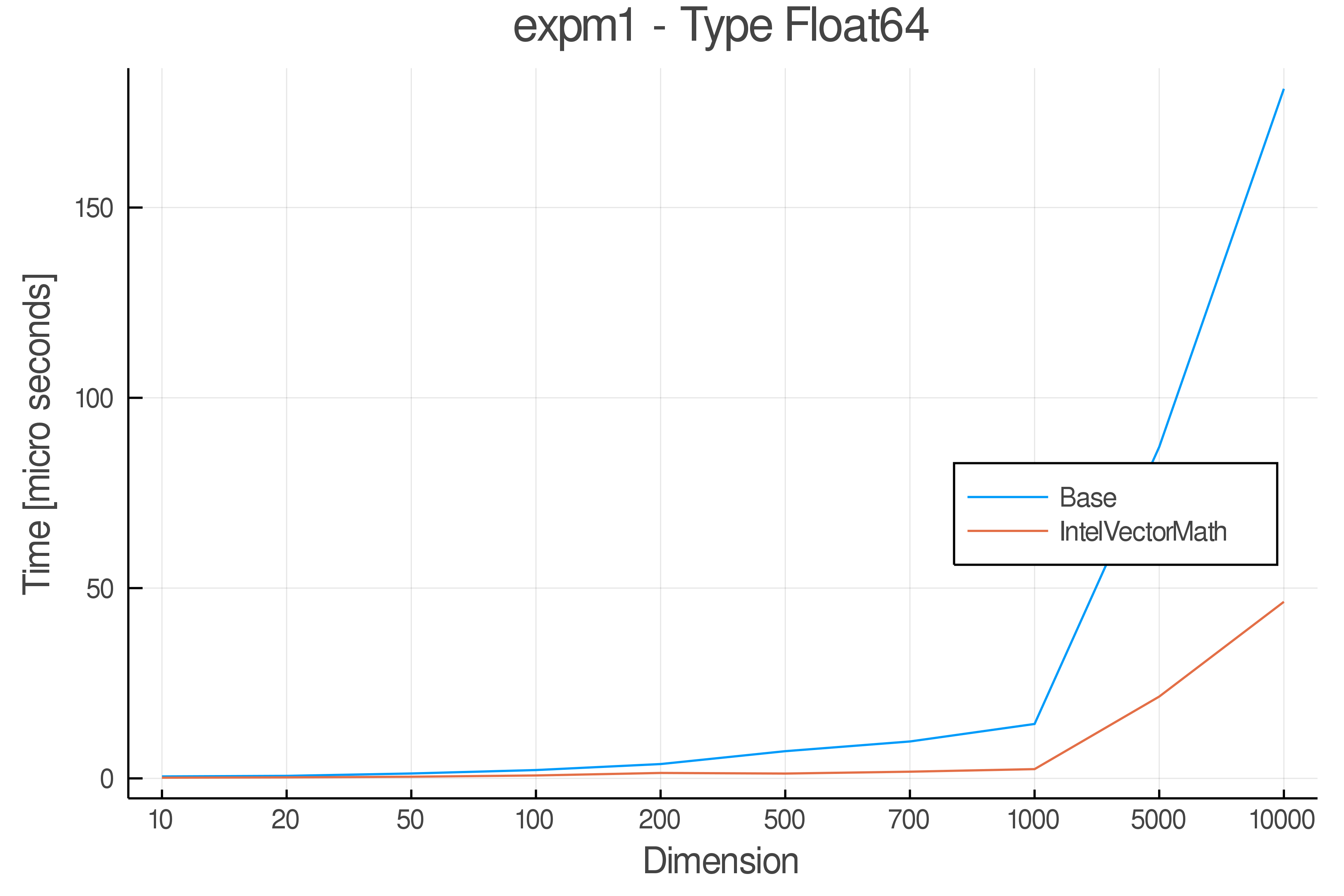
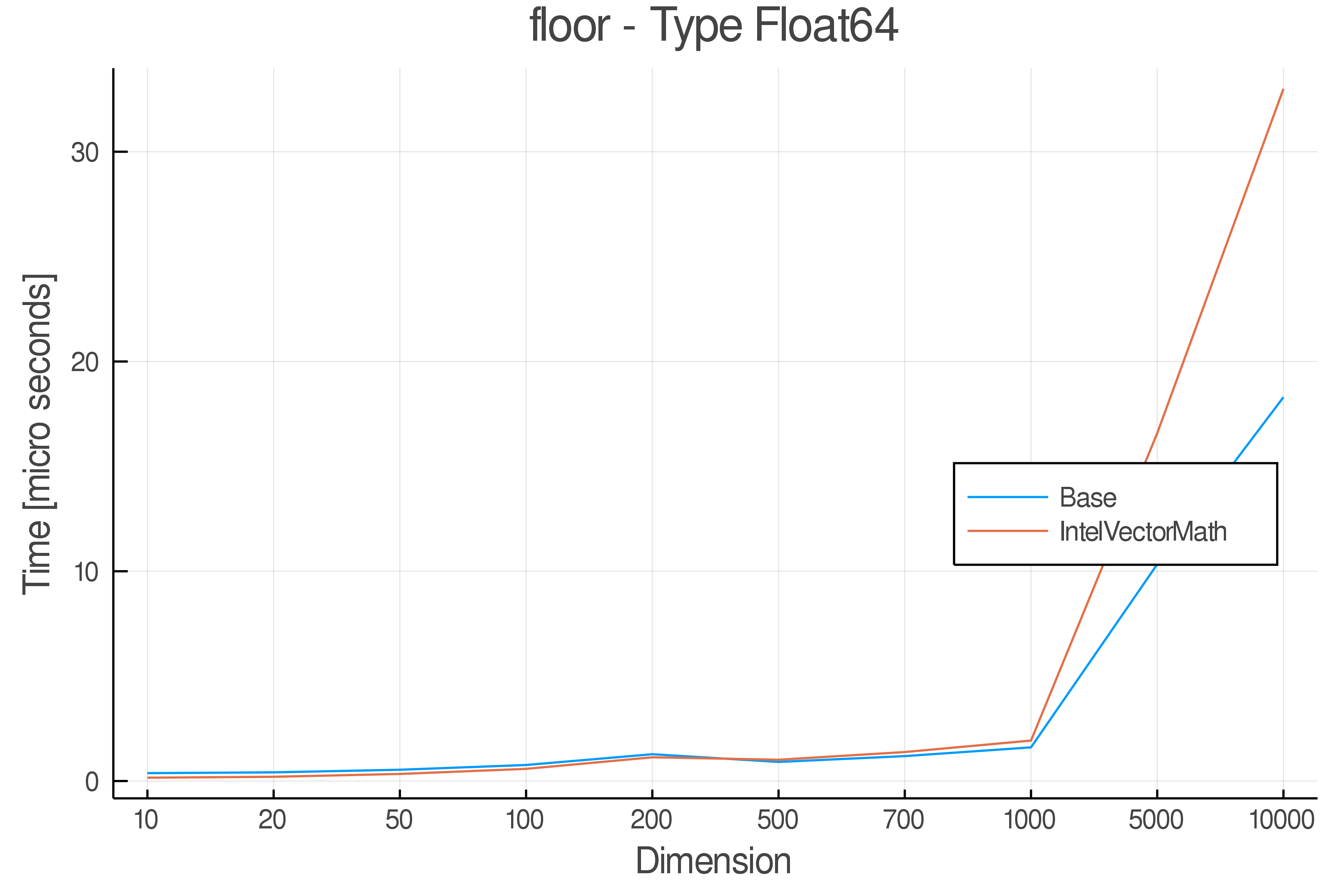
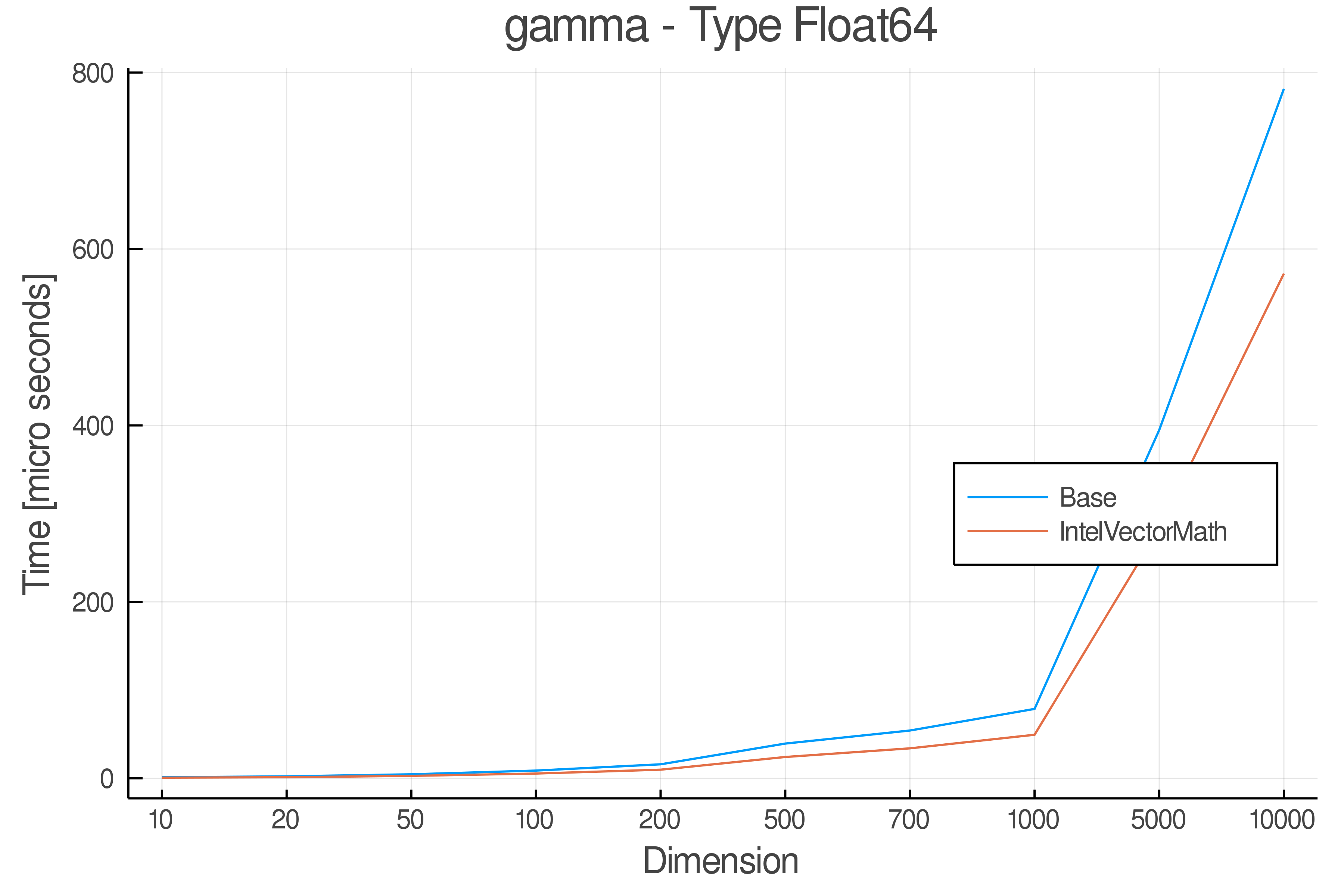
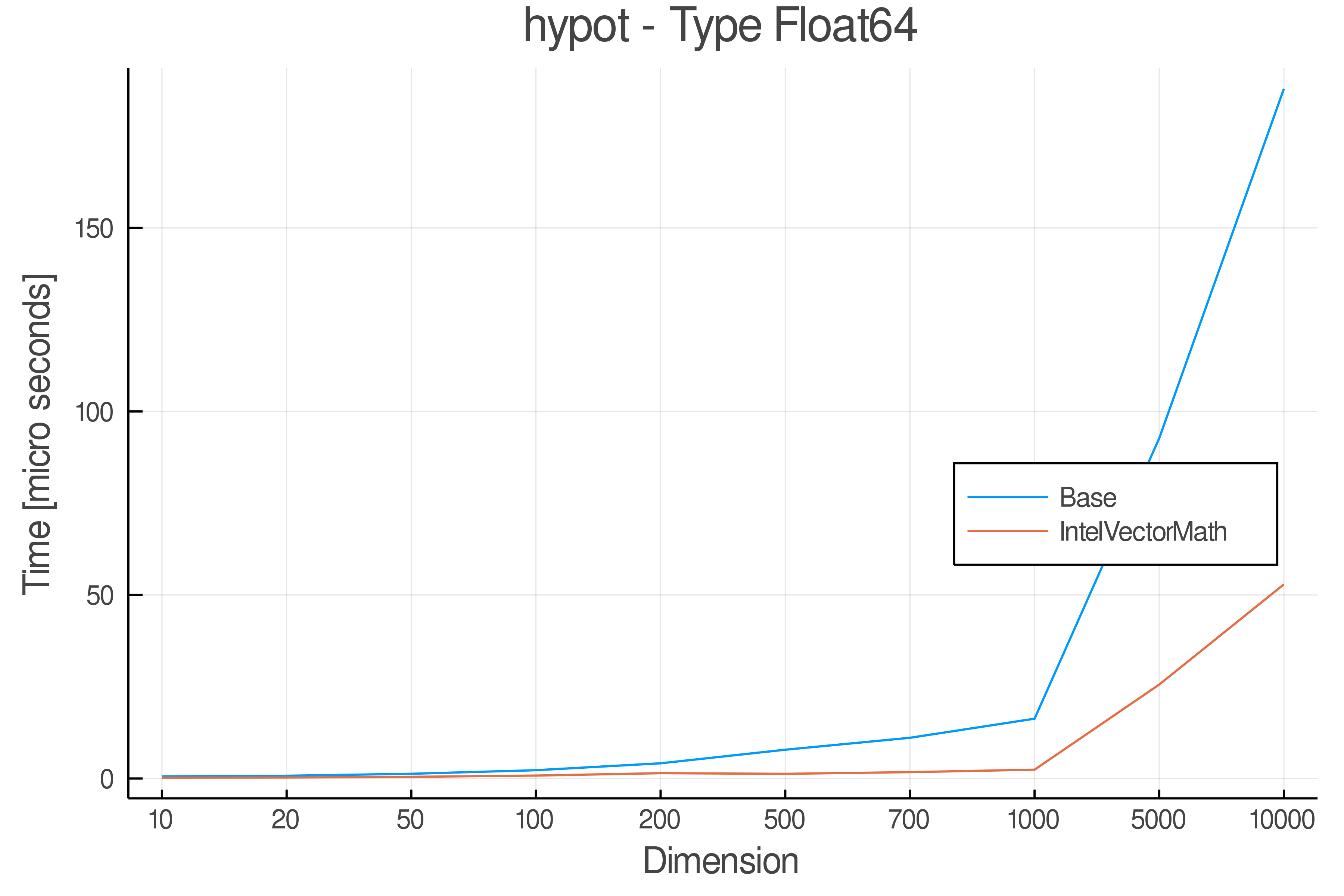
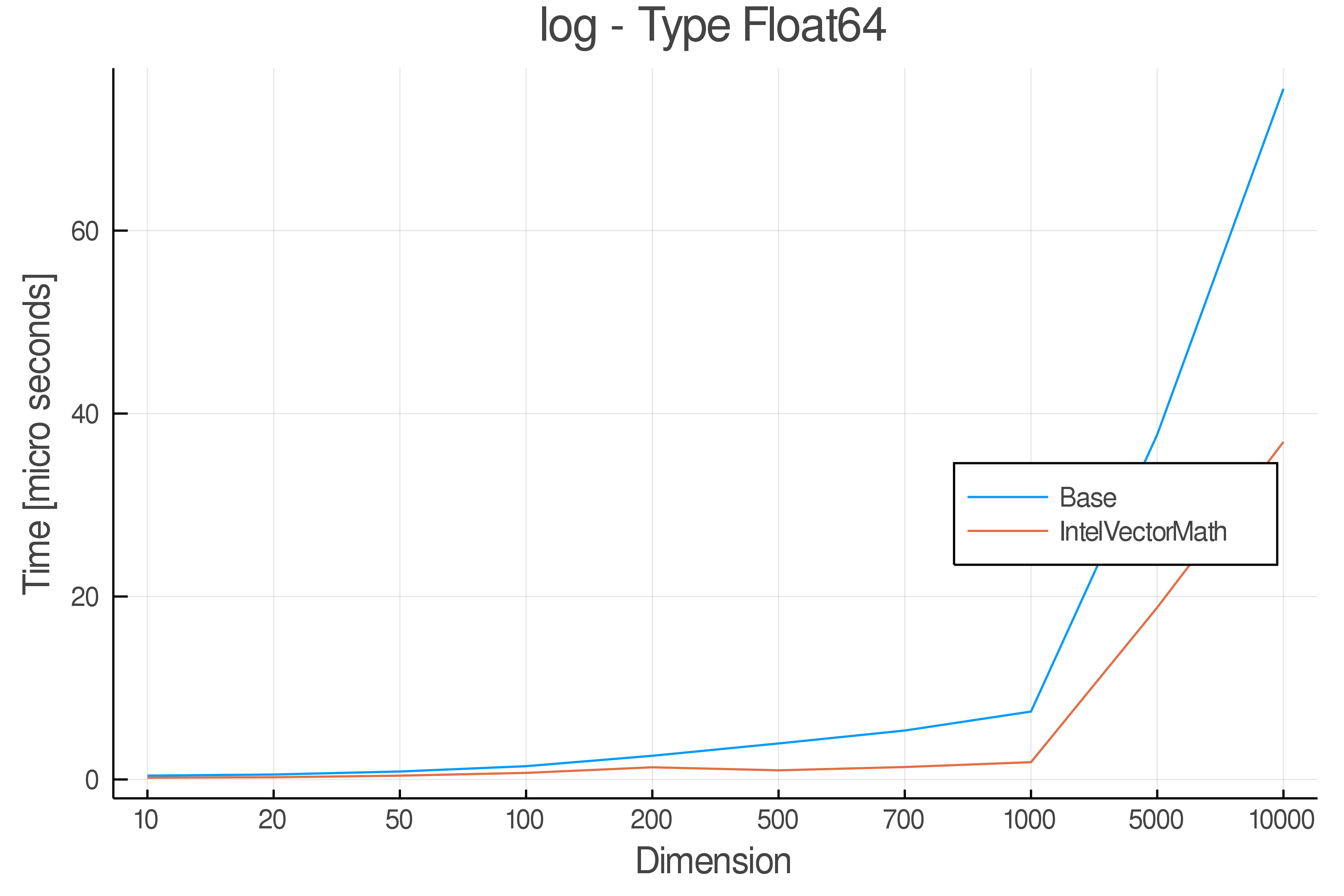
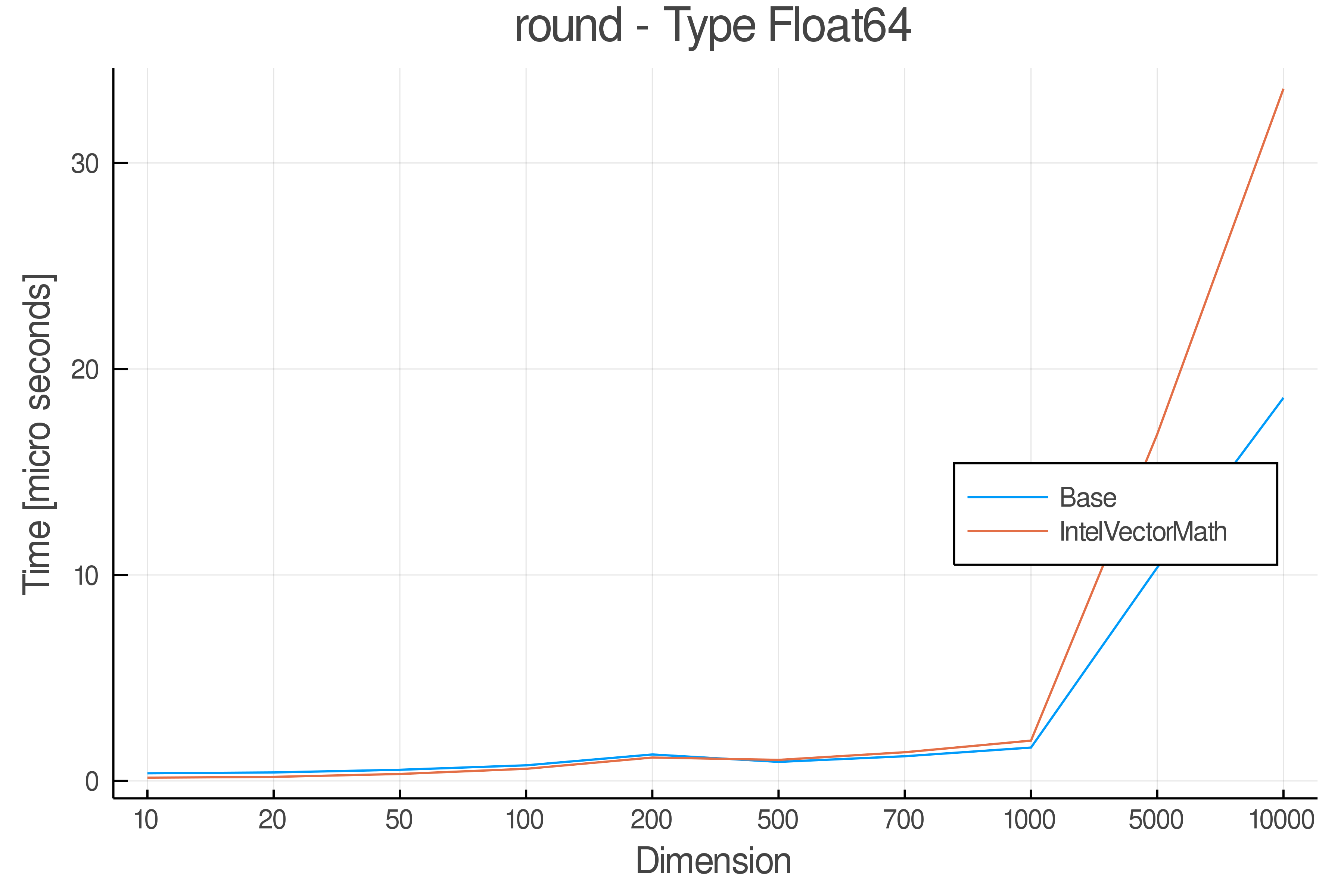
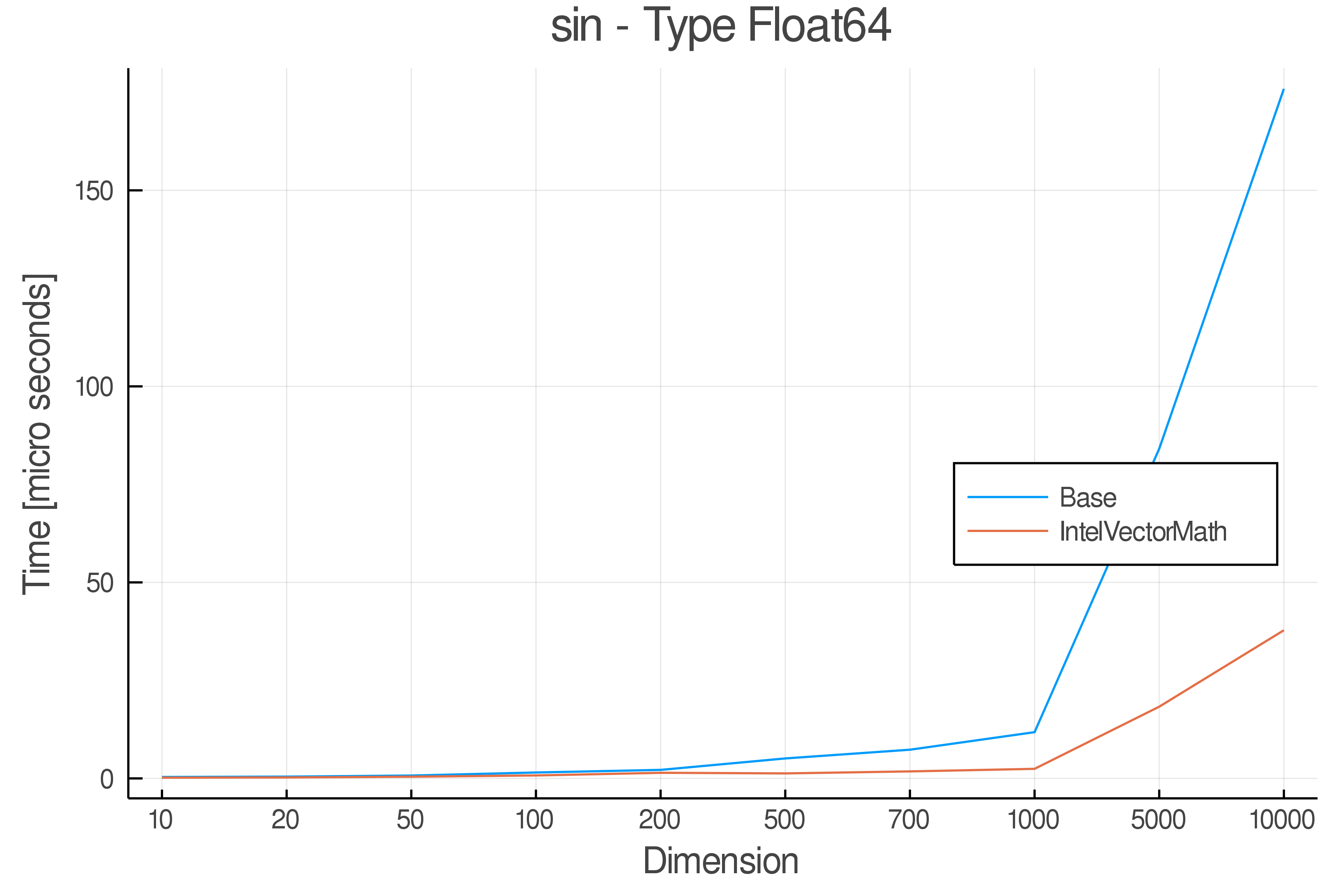
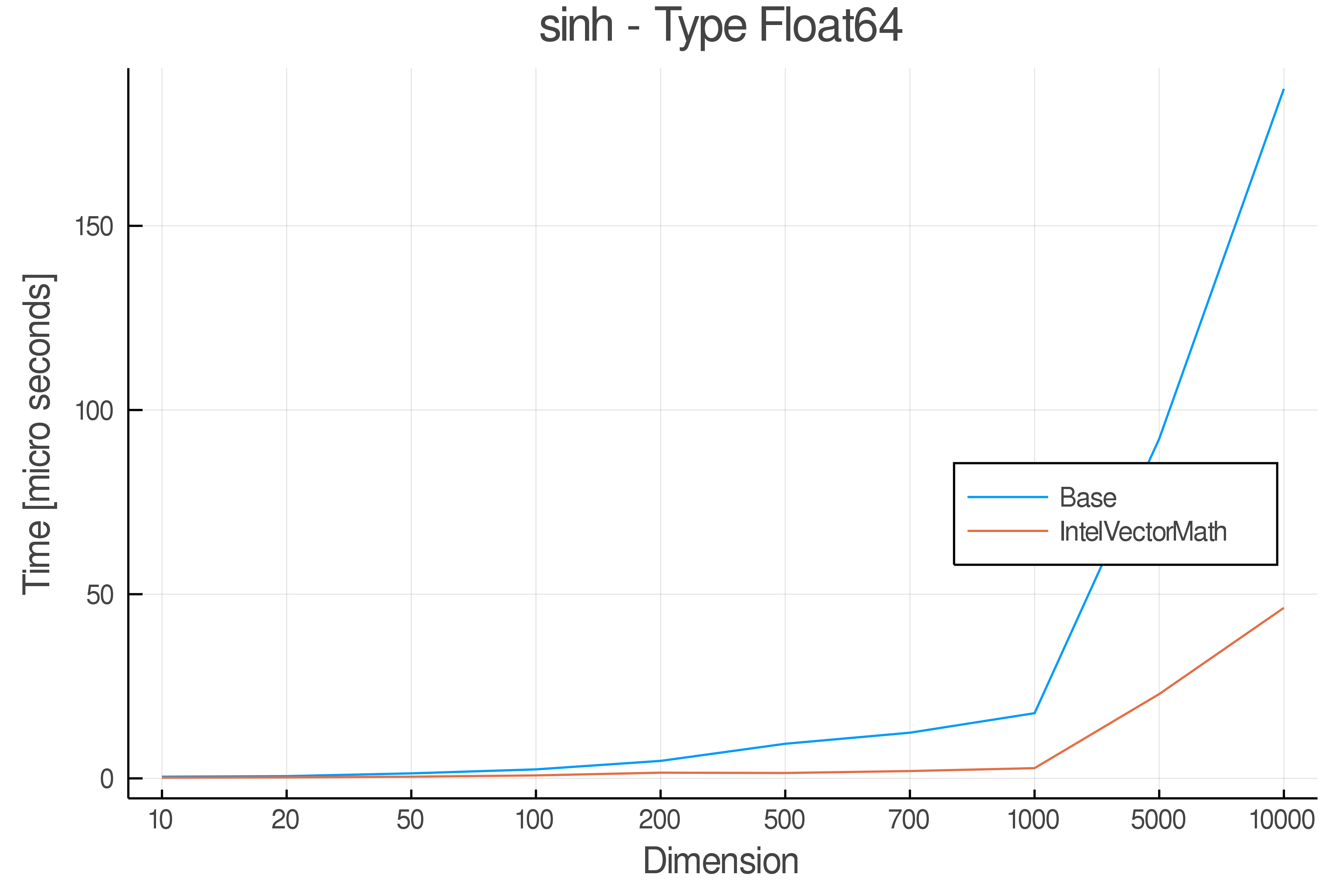
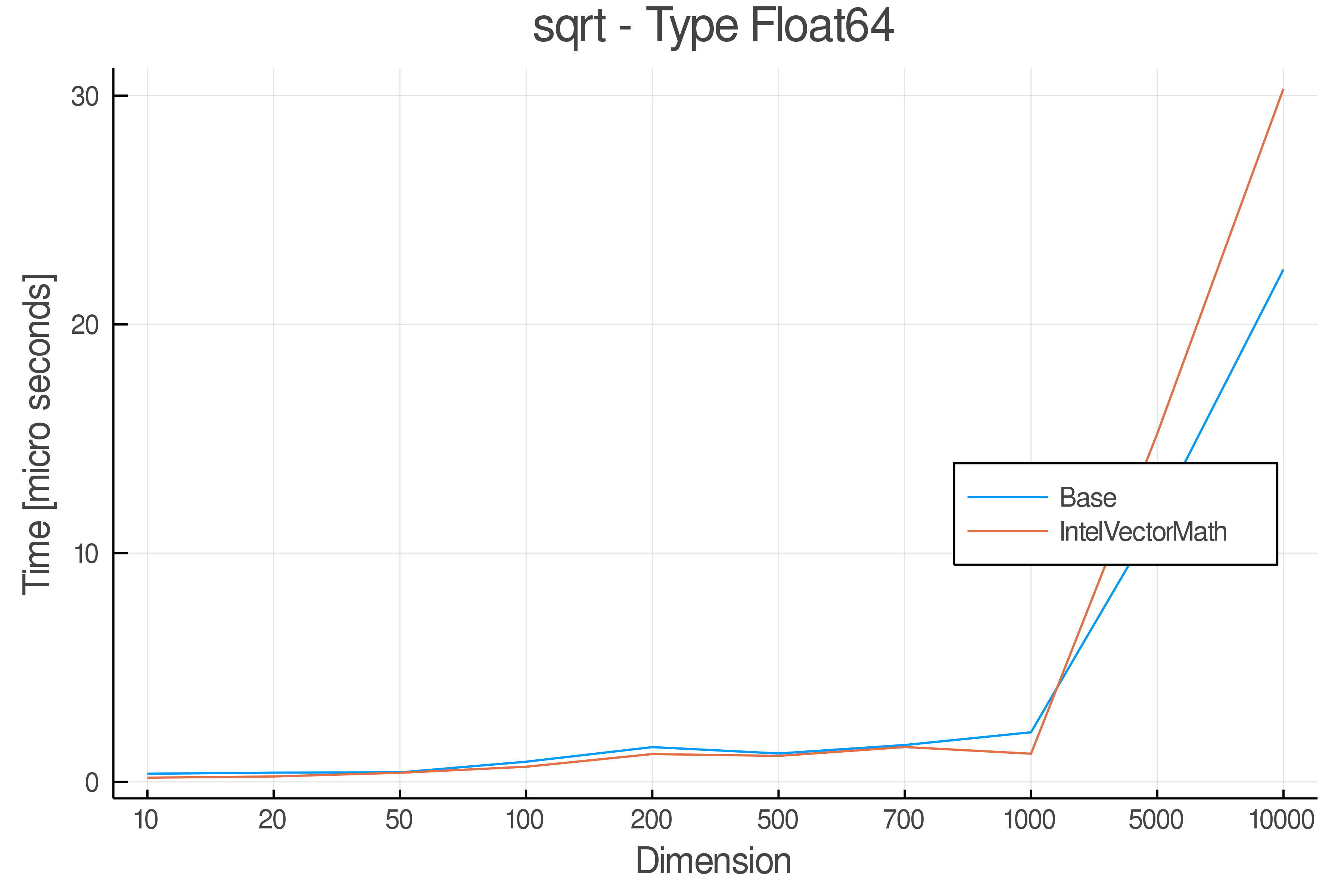
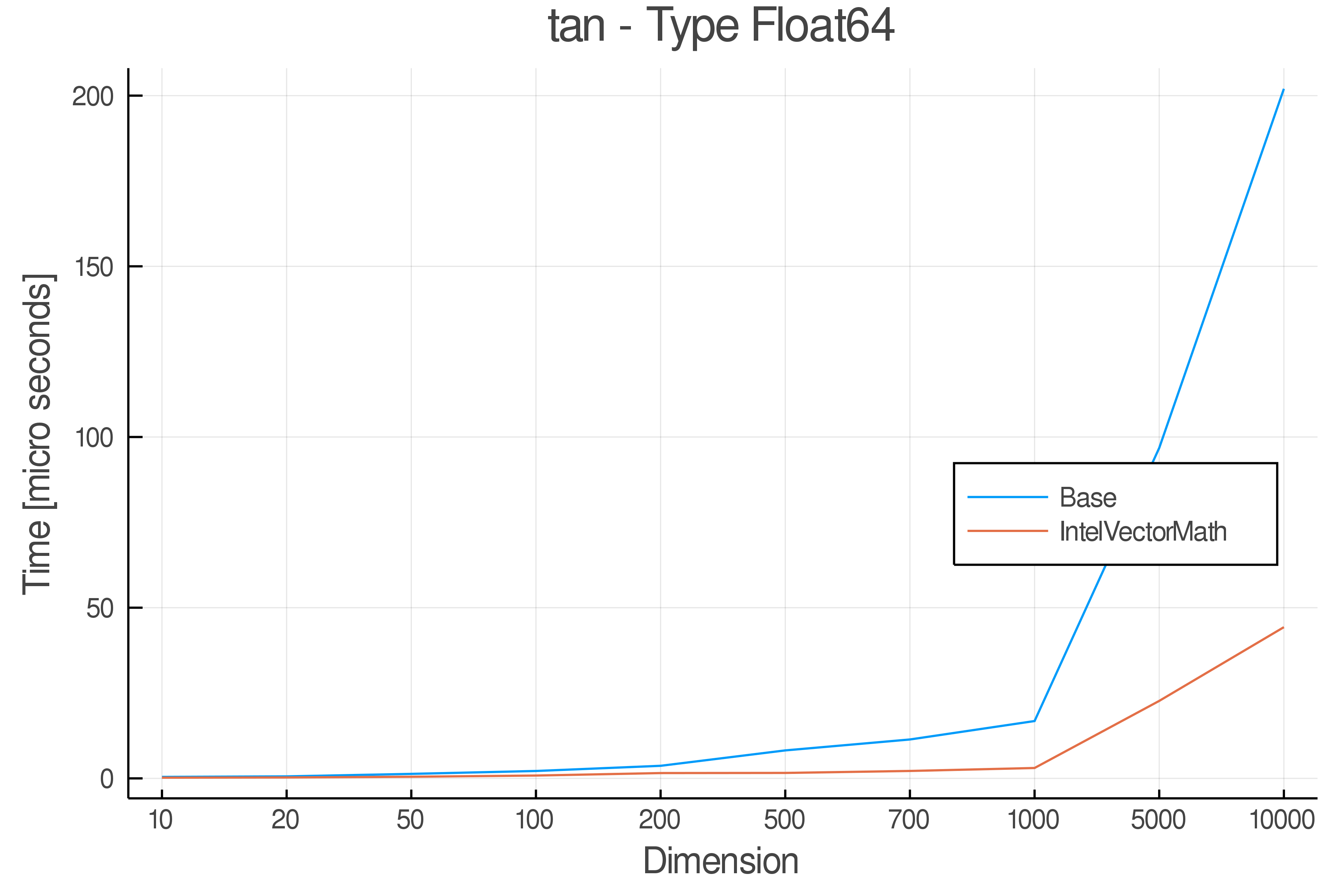
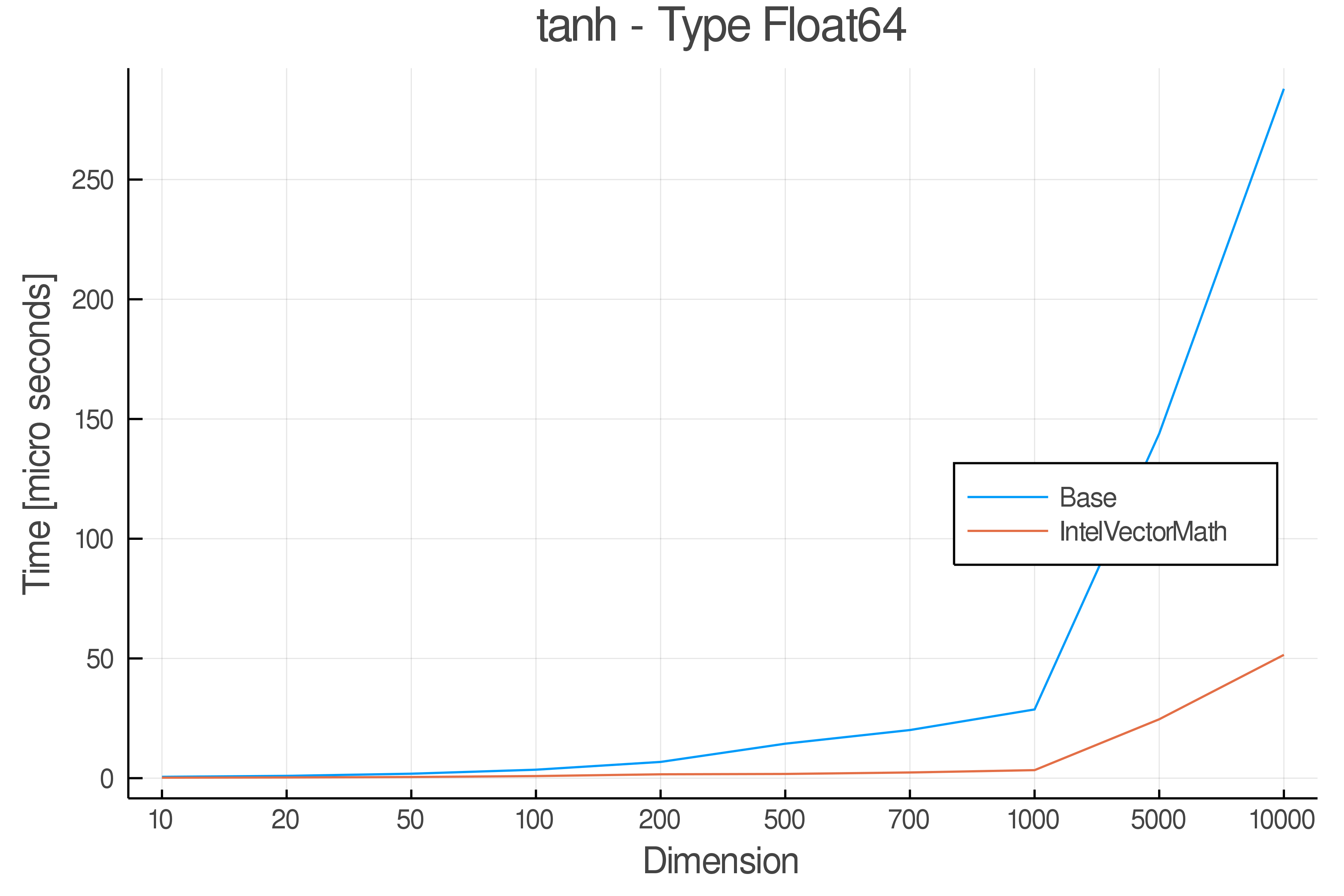
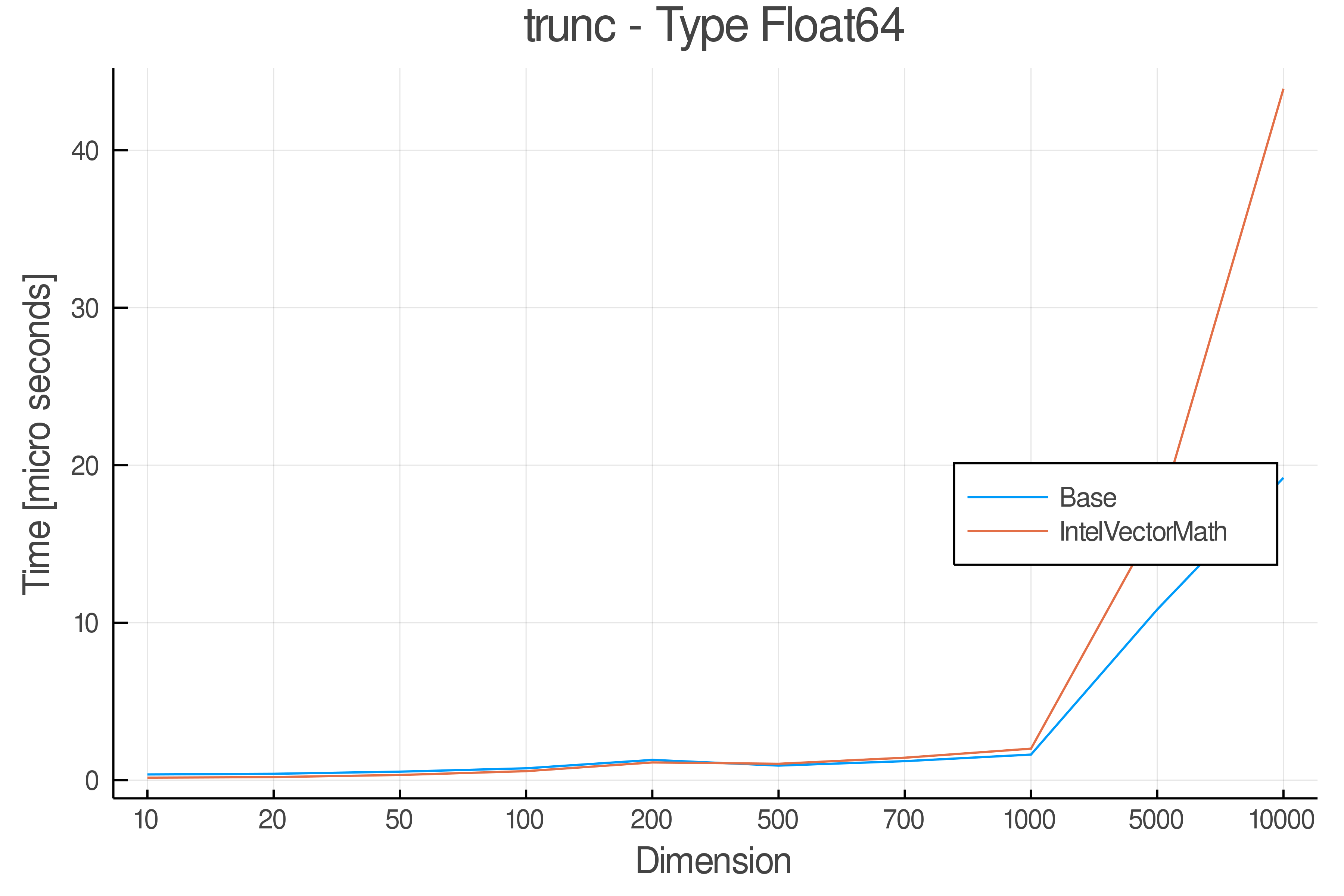
Summary of Results:

Relative speed of IntelVectorMath/Base: The height of the bars is how fast IntelVectorMath is compared to using broadcasting for functions in Base

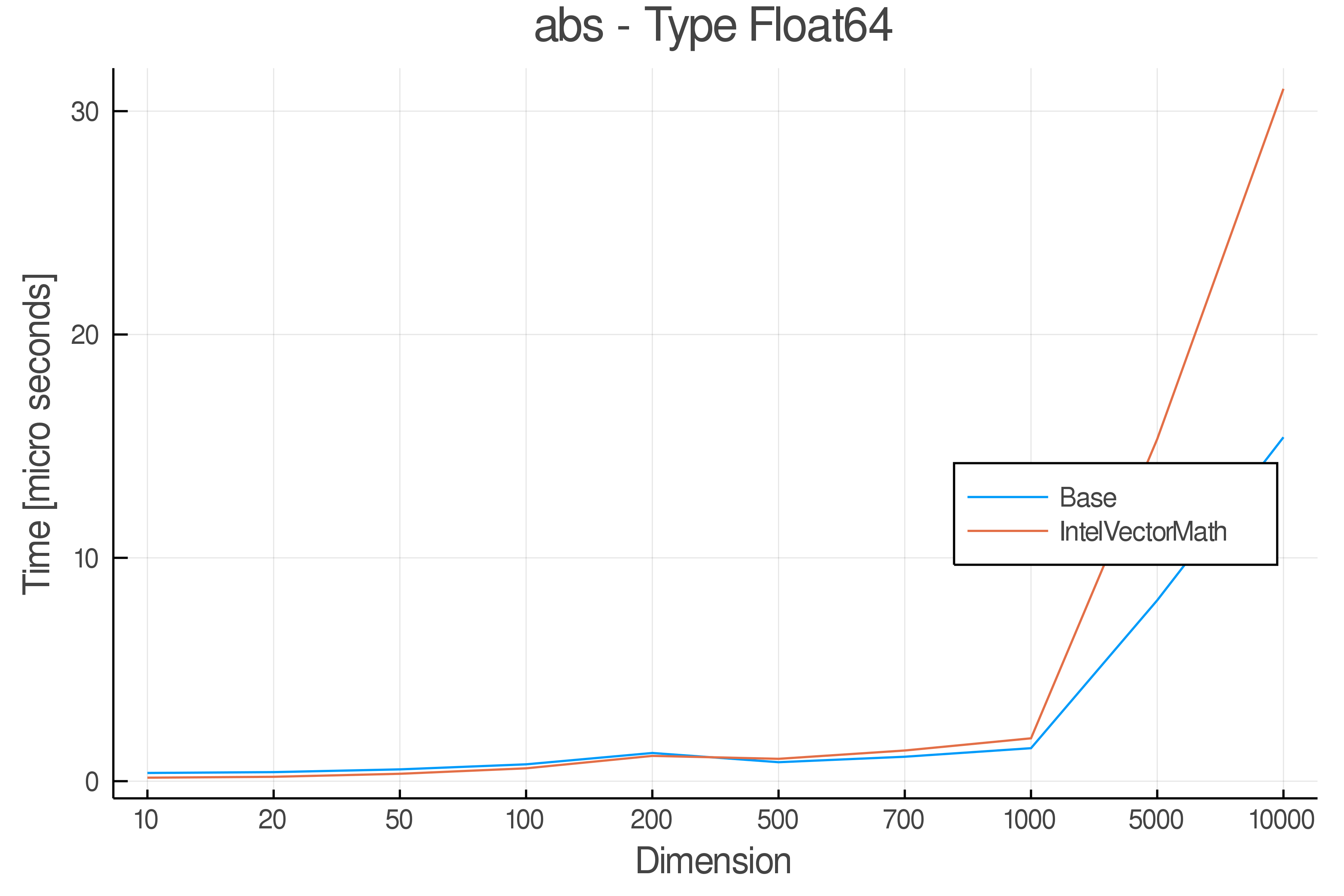
Full Results:

Tests were performed on an Intel(R) Core(TM) i5-8250U @ 1.6 [GHz] 1800 Mhz. The dashed line indicates equivalent performance for IntelVectorMath versus the implementations in Base.

IntelVectorMath.jl supports the following functions, most for Float32 and Float64, while some also take complex numbers.

Allocating forms have signature f(A). Mutating forms have signatures f!(A) (in place) and f!(out, A) (out of place). The last 9 functions have been moved from Base to SpecialFunctions.jl or have no Base equivalent.

Allocating forms have signature f(A, B). Mutating forms have the signature f!(out, A, B).

Next steps for this package

• Windows support
• Basic Testing
• Avoiding overloading base and optional overload function
• Travis and AppVeyor testing
• Adding CIS function
• Move Testing to GitHub Actions
• Add test for using standalone MKL
• Update Benchmarks
• Add tests for mutating functions
• Add own dependency management via BinaryProvider
• Update function list in README
• Adopt Julia 1.3 artifact system, breaking backwards compatibility

1. As a quick help to convert benchmark timings into operations-per-cycle, IntelVectorMath.jl provides vml_get_cpu_frequency() which will return the actual current frequency of the CPU in GHz.

2. Now all IVM functions accept inputs that could be reshaped to an 1d strided array.