BellBruno

Compute Bell polynomials for Faà di Bruno's formula.

N_der = 10;              # Maximum order of Bell polynomial
bp = bell_poly(N_der);   # Create bell polynomials
bc = bell_coeff(bp);     # Compute bell coefficients

Computing and saving Bell polynomials

If you want to compute and save the Bell polynomials you may use

N_der = 20;
path_2_folder = "my_folder_path"
bp = bell_poly( N_der; 
                save_on_disk=true, 
                path_to_folder=path_2_folder, 
                print_iteration=true)

or simply

bp = bell_poly(N_der, save_on_disk = true)

to save the files in folder "bell_results/".

Reading the Bell polynomials

The Bell polynomials can be read with

bp_new = read_bell_poly(path_to_folder=path_2_folder)

or if the standard folder "bell_results/" is used

bp_new = read_bell_poly()

We are wish to find the derivatives of function composition

$$ h(t) = f(g(t)) = \exp(p~\sin(t))$$

up to the order of $N=10$. We assume $p=0.1$.

The derivative of the outer function is noted as

$$ \frac{d^n}{dx^n} f(x) = p^{n} \exp(p~x)$$

and the derivative of the inner function is noted as

$$ \frac{d^n}{dt^n} g(t) = \sin(t+n~\pi/2).$$

Derivative of outer function

p = 0.1;
f_der(x,n) = p^n * exp(p*x) 

Inner function and its derivatives

g(t) = sin(t)
g_der(t,n) = sin(t+n*π/2)

Bell polynomial and coefficients data

using BellBruno
bp = bell_poly(10)
bc = bell_coeff(bp)

Sampling points and Faà di Bruno's formula

tgrid = -π:0.01:2π # Sampling points
diff_data = faa_di_bruno(f_der, g, g_der, tgrid,bp, bc)

The full listing tutorial_example.jl can be found here.

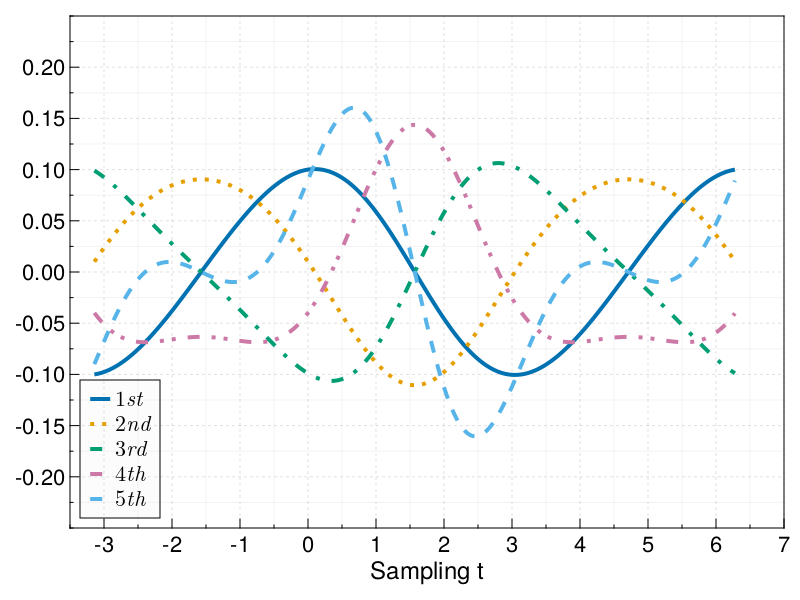
Derivatives up to order 5

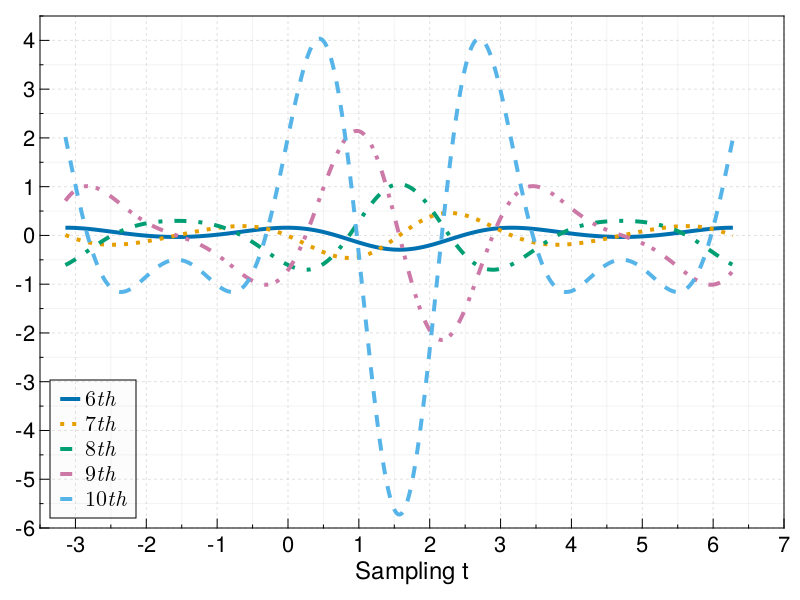
Derivatives up to order 10