deSolveDiffEq.jl is a common interface binding for the R deSolve package of ordinary differential equation solvers. It uses the RCall.jl interop in order to send the differential equation over to R and solve it.
Note that this package isn't for production use and is mostly just for benchmarking and helping new users migrate models over to Julia. For more efficient solvers, see the DifferentialEquations.jl documentation.
To install deSolveDiffEq.jl, use the following:
Pkg.clone("https://github.com/JuliaDiffEq/deSolveDiffEq.jl")Note that this requires that deSolve is already installed from R and that RCall.jl is able to appropriately build.
deSolveDiffEq.jl is simply a solver on the DiffEq common interface, so for details see the DifferentialEquations.jl documentation. The available algorithms are:
deSolveDiffEq.lsoda()
deSolveDiffEq.lsode()
deSolveDiffEq.lsodes()
deSolveDiffEq.lsodar()
deSolveDiffEq.vode()
deSolveDiffEq.daspk()
deSolveDiffEq.euler()
deSolveDiffEq.rk4()
deSolveDiffEq.ode23()
deSolveDiffEq.ode45()
deSolveDiffEq.radau()
deSolveDiffEq.bdf()
deSolveDiffEq.bdf_d()
deSolveDiffEq.adams()
deSolveDiffEq.impAdams()
deSolveDiffEq.impAdams_d()using deSolveDiffEq
function lorenz(u,p,t)
du1 = 10.0(u[2]-u[1])
du2 = u[1]*(28.0-u[3]) - u[2]
du3 = u[1]*u[2] - (8/3)*u[3]
[du1, du2, du3]
end
tspan = (0.0,10.0)
u0 = [1.0,0.0,0.0]
prob = ODEProblem(lorenz,u0,tspan)
sol = solve(prob,deSolveDiffEq.lsoda())deSolveDiffEq.jl has about a 2x-3x overhead over using deSolve in R directly. To see this, we can time the main example from the website
library(deSolve)
Lorenz <- function(t, state, parameters) {
with(as.list(c(state, parameters)), {
dX <- a * X + Y * Z
dY <- b * (Y - Z)
dZ <- -X * Y + c * Y - Z
list(c(dX, dY, dZ))
})
}
parameters <- c(a = -8/3, b = -10, c = 28)
state <- c(X = 1, Y = 1, Z = 1)
times <- seq(0, 100, by = 0.01)
system.time(out <- ode(y = state, times = times, func = Lorenz, parms = parameters))which outputs
RObject{RealSxp}
user system elapsed
0.33 0.00 0.33
vs the deSolveDiffEq.jl approach:
using deSolveDiffEq, BenchmarkTools
function lorenz(u,p,t)
du1 = 10.0(u[2]-u[1])
du2 = u[1]*(28.0-u[3]) - u[2]
du3 = u[1]*u[2] - (8/3)*u[3]
[du1, du2, du3]
end
u0 = [1.0;0.0;0.0]
tspan = (0.0,100.0)
prob = ODEProblem(lorenz,u0,tspan)
@btime sol = solve(prob,deSolveDiffEq.lsoda()) # 812.972 ms (2152395 allocations: 67.85 MiB)Note that the implementation requires that the function returns a list, so an R list is generated on the output of each user function call. This means this is more comparable to the timings of the standard deSolve usage, and not the C/Fortran function version. We are working to see if that interface can be directly accessible by Julia functions to check the "expert's version" call overhead
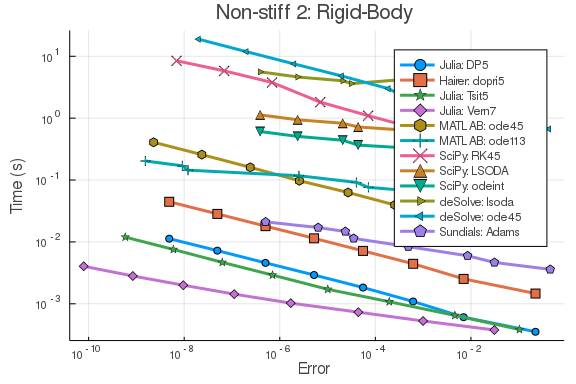
The following benchmarks demonstrate a 1000x performance advantage for the pure-Julia methods over the deSolve ODE solvers across a range of stiff and non-stiff ODEs*. These were ran with Julia 1.2, MATLAB 2019B, deSolve 1.2.5, and SciPy 1.3.1 after verifying negligible overhead on interop.
* There is a caveat: this is comparing the "R form" code vs the pure Julia code. If one directly writes C/Fortran files and compiles that using the compiled code interface, the deSolve LSODA matches the performance of LSODA.jl and other pure C/Fortran calls. Thus this only applied to the standard deSolve usage.
f = @ode_def_bare LotkaVolterra begin
dx = a*x - b*x*y
dy = -c*y + d*x*y
end a b c d
p = [1.5,1,3,1]
tspan = (0.0,10.0)
u0 = [1.0,1.0]
prob = ODEProblem(f,u0,tspan,p)
sol = solve(prob,Vern7(),abstol=1/10^14,reltol=1/10^14)
test_sol = TestSolution(sol)
setups = [Dict(:alg=>DP5())
Dict(:alg=>dopri5())
Dict(:alg=>Tsit5())
Dict(:alg=>Vern7())
Dict(:alg=>MATLABDiffEq.ode45())
Dict(:alg=>MATLABDiffEq.ode113())
Dict(:alg=>SciPyDiffEq.RK45())
Dict(:alg=>SciPyDiffEq.LSODA())
Dict(:alg=>SciPyDiffEq.odeint())
Dict(:alg=>deSolveDiffEq.lsoda())
Dict(:alg=>deSolveDiffEq.ode45())
Dict(:alg=>CVODE_Adams())
]
names = [
"Julia: DP5"
"Hairer: dopri5"
"Julia: Tsit5"
"Julia: Vern7"
"MATLAB: ode45"
"MATLAB: ode113"
"SciPy: RK45"
"SciPy: LSODA"
"SciPy: odeint"
"deSolve: lsoda"
"deSolve: ode45"
"Sundials: Adams"
]
abstols = 1.0 ./ 10.0 .^ (6:13)
reltols = 1.0 ./ 10.0 .^ (3:10)
wp = WorkPrecisionSet(prob,abstols,reltols,setups;
names = names,
appxsol=test_sol,dense=false,
save_everystep=false,numruns=100,maxiters=10000000,
timeseries_errors=false,verbose=false)
plot(wp,title="Non-stiff 1: Lotka-Volterra")f = @ode_def_bare RigidBodyBench begin
dy1 = -2*y2*y3
dy2 = 1.25*y1*y3
dy3 = -0.5*y1*y2 + 0.25*sin(t)^2
end
prob = ODEProblem(f,[1.0;0.0;0.9],(0.0,100.0))
sol = solve(prob,Vern7(),abstol=1/10^14,reltol=1/10^14)
test_sol = TestSolution(sol)
setups = [Dict(:alg=>DP5())
Dict(:alg=>dopri5())
Dict(:alg=>Tsit5())
Dict(:alg=>Vern7())
Dict(:alg=>MATLABDiffEq.ode45())
Dict(:alg=>MATLABDiffEq.ode113())
Dict(:alg=>SciPyDiffEq.RK45())
Dict(:alg=>SciPyDiffEq.LSODA())
Dict(:alg=>SciPyDiffEq.odeint())
Dict(:alg=>deSolveDiffEq.lsoda())
Dict(:alg=>deSolveDiffEq.ode45())
Dict(:alg=>CVODE_Adams())
]
names = [
"Julia: DP5"
"Hairer: dopri5"
"Julia: Tsit5"
"Julia: Vern7"
"MATLAB: ode45"
"MATLAB: ode113"
"SciPy: RK45"
"SciPy: LSODA"
"SciPy: odeint"
"deSolve: lsoda"
"deSolve: ode45"
"Sundials: Adams"
]
abstols = 1.0 ./ 10.0 .^ (6:13)
reltols = 1.0 ./ 10.0 .^ (3:10)
wp = WorkPrecisionSet(prob,abstols,reltols,setups;
names = names,
appxsol=test_sol,dense=false,
save_everystep=false,numruns=100,maxiters=10000000,
timeseries_errors=false,verbose=false)
plot(wp,title="Non-stiff 2: Rigid-Body")rober = @ode_def begin
dy₁ = -k₁*y₁+k₃*y₂*y₃
dy₂ = k₁*y₁-k₂*y₂^2-k₃*y₂*y₃
dy₃ = k₂*y₂^2
end k₁ k₂ k₃
prob = ODEProblem(rober,[1.0,0.0,0.0],(0.0,1e5),[0.04,3e7,1e4])
sol = solve(prob,CVODE_BDF(),abstol=1/10^14,reltol=1/10^14)
test_sol = TestSolution(sol)
abstols = 1.0 ./ 10.0 .^ (7:8)
reltols = 1.0 ./ 10.0 .^ (3:4);
setups = [Dict(:alg=>Rosenbrock23())
Dict(:alg=>TRBDF2())
Dict(:alg=>RadauIIA5())
Dict(:alg=>rodas())
Dict(:alg=>radau())
Dict(:alg=>MATLABDiffEq.ode23s())
Dict(:alg=>MATLABDiffEq.ode15s())
Dict(:alg=>SciPyDiffEq.LSODA())
Dict(:alg=>SciPyDiffEq.BDF())
Dict(:alg=>SciPyDiffEq.odeint())
Dict(:alg=>deSolveDiffEq.lsoda())
Dict(:alg=>CVODE_BDF())
]
names = [
"Julia: Rosenbrock23"
"Julia: TRBDF2"
"Julia: radau"
"Hairer: rodas"
"Hairer: radau"
"MATLAB: ode23s"
"MATLAB: ode15s"
"SciPy: LSODA"
"SciPy: BDF"
"SciPy: odeint"
"deSolve: lsoda"
"Sundials: CVODE"
]
wp = WorkPrecisionSet(prob,abstols,reltols,setups;
names = names,print_names = true,
dense=false,verbose = false,
save_everystep=false,appxsol=test_sol,
maxiters=Int(1e5))
plot(wp,title="Stiff 1: ROBER", legend=:topleft)f = @ode_def Hires begin
dy1 = -1.71*y1 + 0.43*y2 + 8.32*y3 + 0.0007
dy2 = 1.71*y1 - 8.75*y2
dy3 = -10.03*y3 + 0.43*y4 + 0.035*y5
dy4 = 8.32*y2 + 1.71*y3 - 1.12*y4
dy5 = -1.745*y5 + 0.43*y6 + 0.43*y7
dy6 = -280.0*y6*y8 + 0.69*y4 + 1.71*y5 -
0.43*y6 + 0.69*y7
dy7 = 280.0*y6*y8 - 1.81*y7
dy8 = -280.0*y6*y8 + 1.81*y7
end
u0 = zeros(8)
u0[1] = 1
u0[8] = 0.0057
prob = ODEProblem(f,u0,(0.0,321.8122))
sol = solve(prob,Rodas5(),abstol=1/10^14,reltol=1/10^14)
test_sol = TestSolution(sol)
abstols = 1.0 ./ 10.0 .^ (5:8)
reltols = 1.0 ./ 10.0 .^ (1:4);
setups = [Dict(:alg=>Rosenbrock23())
Dict(:alg=>TRBDF2())
Dict(:alg=>RadauIIA5())
Dict(:alg=>rodas())
Dict(:alg=>radau())
Dict(:alg=>MATLABDiffEq.ode23s())
Dict(:alg=>MATLABDiffEq.ode15s())
Dict(:alg=>SciPyDiffEq.LSODA())
Dict(:alg=>SciPyDiffEq.BDF())
Dict(:alg=>SciPyDiffEq.odeint())
Dict(:alg=>deSolveDiffEq.lsoda())
Dict(:alg=>CVODE_BDF())
]
names = [
"Julia: Rosenbrock23"
"Julia: TRBDF2"
"Julia: radau"
"Hairer: rodas"
"Hairer: radau"
"MATLAB: ode23s"
"MATLAB: ode15s"
"SciPy: LSODA"
"SciPy: BDF"
"SciPy: odeint"
"deSolve: lsoda"
"Sundials: CVODE"
]
wp = WorkPrecisionSet(prob,abstols,reltols,setups;
names = names,print_names = true,
save_everystep=false,appxsol=test_sol,
maxiters=Int(1e5),numruns=100)
plot(wp,title="Stiff 2: Hires",legend=:topleft)