Metaheuristics

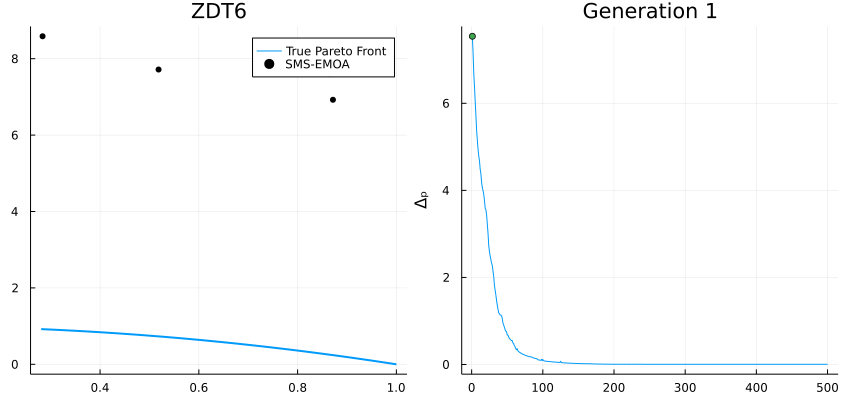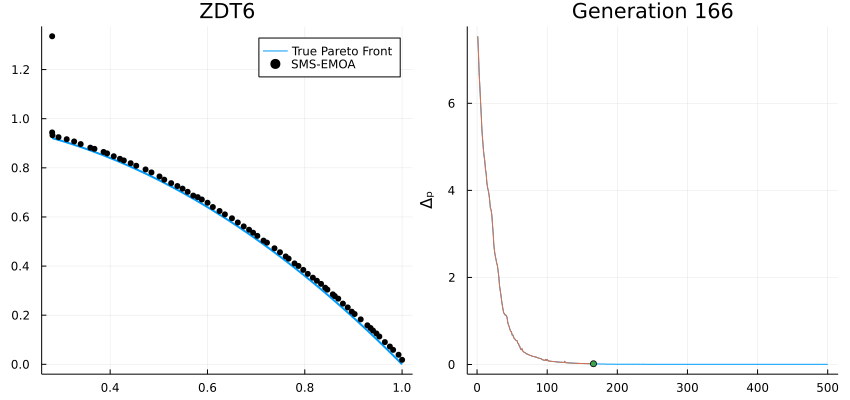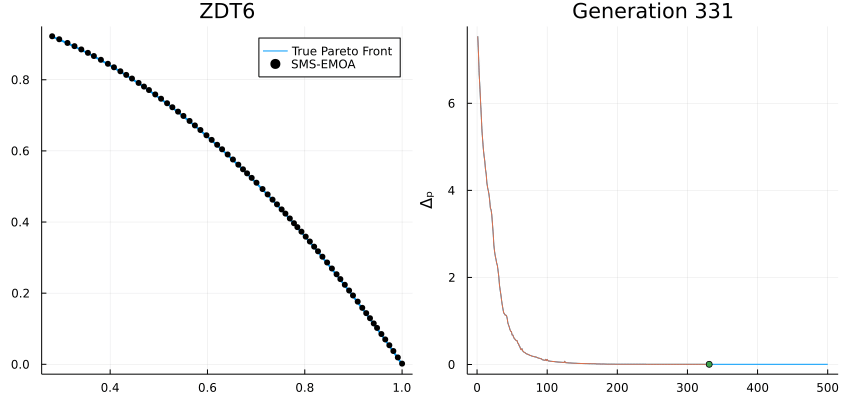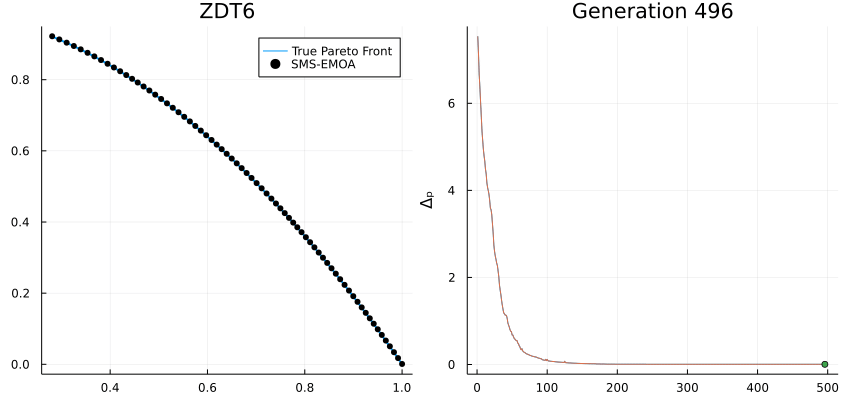
High-performance metaheuristics for global optimization.

Open the Julia REPL and press ] to open the Pkg prompt. To add this package, use the add command:

pkg> add Metaheuristics

Or, equivalently, via the Pkg API:

julia> import Pkg; Pkg.add("Metaheuristics")

Some representative metaheuristics are developed here, including those for single- and multi-objective optimization. Moreover, some constraint handling techniques have been considered in most of the implemented algorithms.

• GRASP: Greedy randomized adaptive search procedure.
• VND: Variable Neighborhood Descent.
• VNS: Variable Neighborhood Search.
• BRKGA: Biased Random Key Genetic Algorithm.

• ECA: Evolutionary Centers Algorithm
• DE: Differential Evolution
• PSO: Particle Swarm Optimization
• SA: Simulated Annealing
• MCCGA: Machine-coded Compact Genetic Algorithm
• GA: Genetic Algorithm
• and more...

• MOEA/D-DE: Multi-objective Evolutionary Algorithm based on Decomposition
• NSGA-II: A fast and elitist multi-objective genetic algorithm: NSGA-II
• NSGA-III: Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach
• SMS-EMOA: An EMO algorithm using the hypervolume measure as the selection criterion
• SPEA2: Improved Strength Pareto Evolutionary Algorithm
• CCMO: Coevolutionary Framework for Constrained Multiobjective Optimization

• GD: Generational Distance
• IGD, IGD+: Inverted Generational Distance (Plus)
• C-metric: Covering Indicator
• HV: Hypervolume
• Δₚ (Delta p): Averaged Hausdorff distance
• Spacing Indicator
• and more...

Multi-Criteria Decision Making methods are available, including:

• Compromise Programming
• Region of Interest Archiving
• Interface for JMcDM (a package for Multiple-criteria decision-making)

Assume you want to solve the following minimization problem.

Minimize:

$$f(x) = 10D + \sum_{i=1}^D x_i^2 - 10\cos(2\pi x_i)$$

where $x\in [-5, 5]^D$, that is, each coordinate in $x$ is between -5 and 5. Use $D=10$.

Firstly, import the Metaheuristics package:

using Metaheuristics

Code the objective function:

f(x) = 10length(x) + sum( x.^2 - 10cos.(2π*x)  )

Instantiate the bounds:

D = 10
bounds = boxconstraints(lb = -5ones(D), ub = 5ones(D))

Also, bounds can be a $2\times 10$ Matrix where the first row corresponds to the lower bounds whilst the second row corresponds to the upper bounds.

Approximate the optimum using the function optimize.

result = optimize(f, bounds)

Optimize returns a State datatype which contains some information about the approximation. For instance, you may use mainly two functions to obtain such an approximation.

@show minimum(result)
@show minimizer(result)

See the documentation for more details, examples and options.

Please cite the package using the bibtex entry

@article{metaheuristics2022, 
  doi = {10.21105/joss.04723}, 
  url = {https://doi.org/10.21105/joss.04723}, 
  year = {2022}, 
  publisher = {The Open Journal}, 
  volume = {7}, 
  number = {78}, 
  pages = {4723}, 
  author = {Jesús-Adolfo Mejía-de-Dios and Efrén Mezura-Montes}, 
  title = {Metaheuristics: A Julia Package for Single- and Multi-Objective Optimization}, 
 journal = {Journal of Open Source Software} }

or the citation string

Mejía-de-Dios et al., (2022). Metaheuristics: A Julia Package for Single- and Multi-Objective Optimization. Journal of Open Source Software, 7(78), 4723, https://doi.org/10.21105/joss.04723

in your scientific paper if you use Metaheristics.jl.

Please feel free to send me your PR, issue or any comment about this package for Julia.