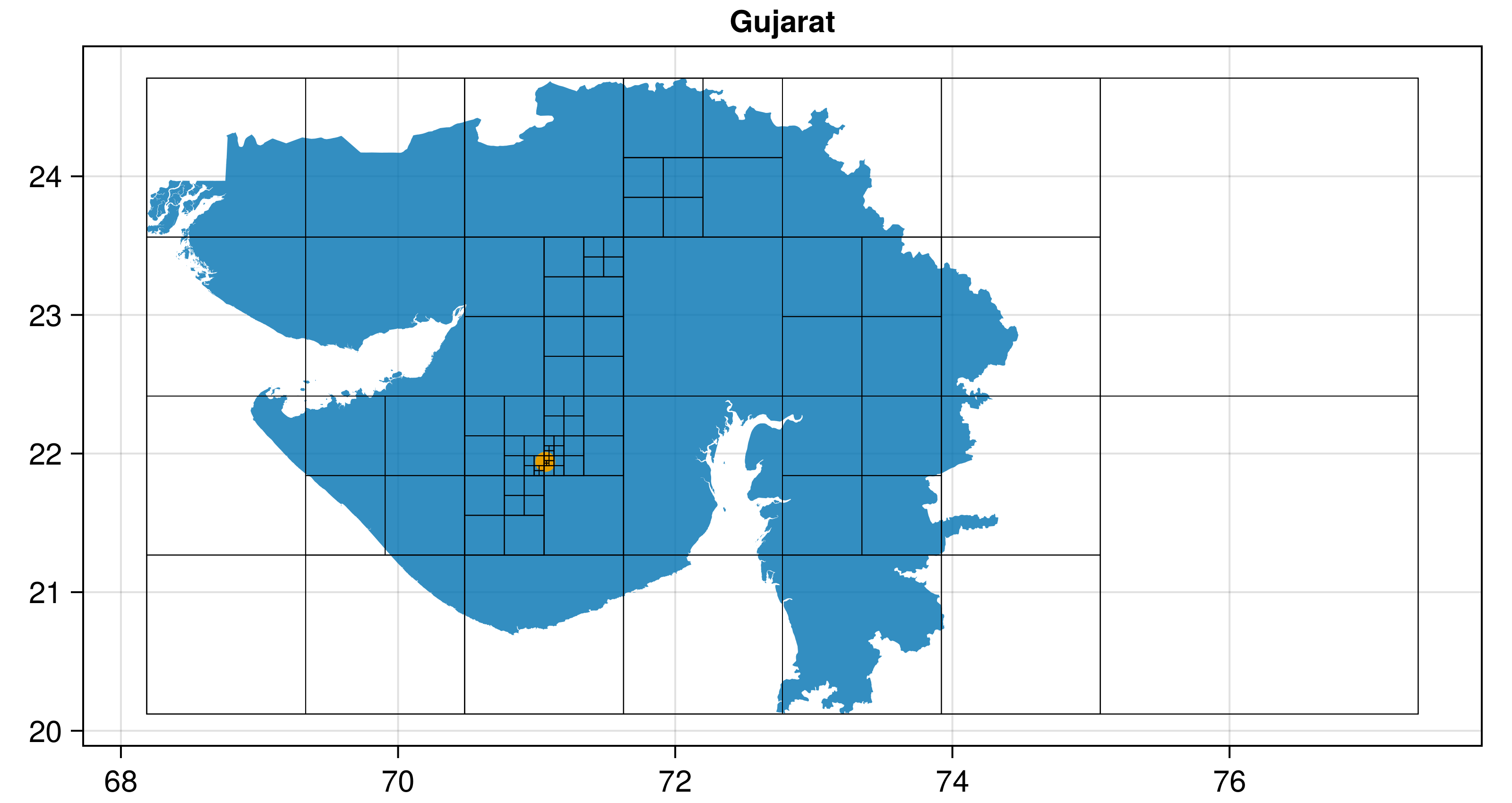
Polylabel.jl

This package implements an algorithm to find the pole of inaccessibility of a polygon, the most distant internal point from the polygon outline. This algorithm was originally written (and taken from) mapbox/polylabel - you can find a lot more information there! To summarize, the algorithm is basically a quad-tree search across the polygon which finds the point which is most distant from any edge.

In the plot above, this point is shown in orange, while the input polygon (multipolygon in this case) is shown in blue.

The package is built on top of the GeoInterface, and is built to work with any polygons or multipolygon object which implements the GeoInterface, specifically the functions GeoInterface.contains, GeoInterface.centroid, and the geointerface_geomtype API for reverse conversion.

The main entry point is the polylabel(input; atol = nothing, rtol = 0.01) function. It returns a 2-Tuple of floats, representing the x and y coordinates of the found pole of inaccessibility.