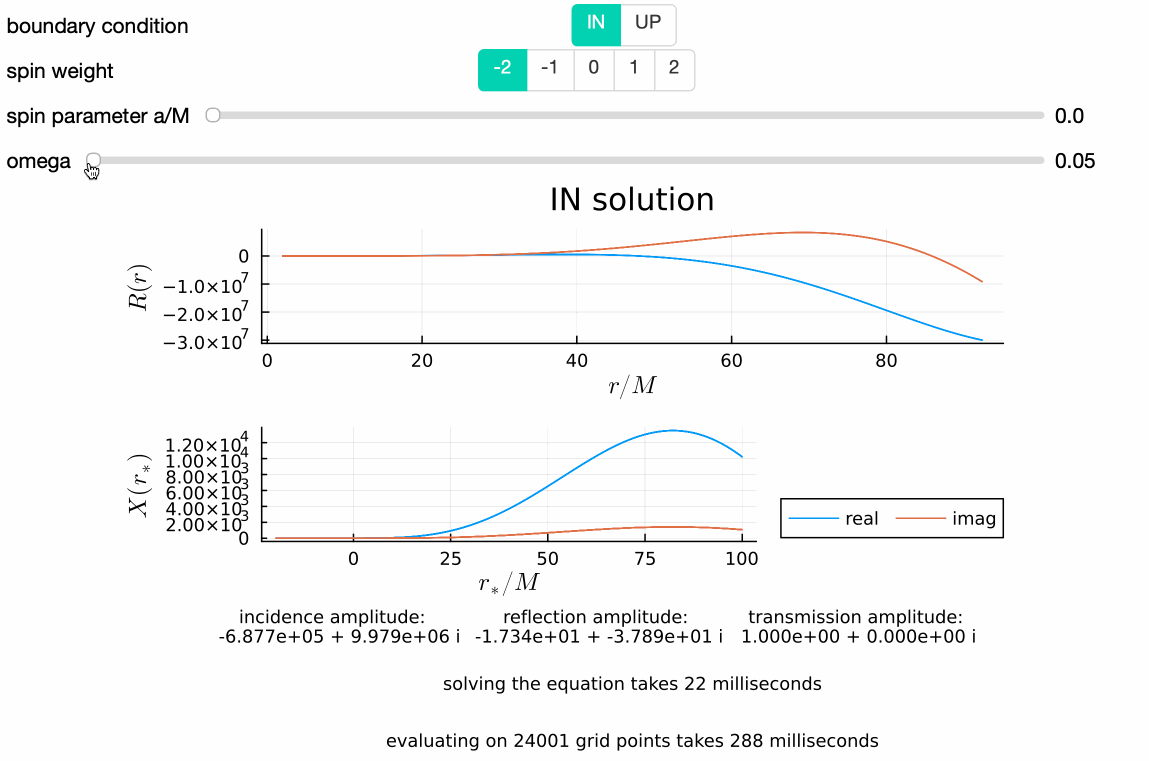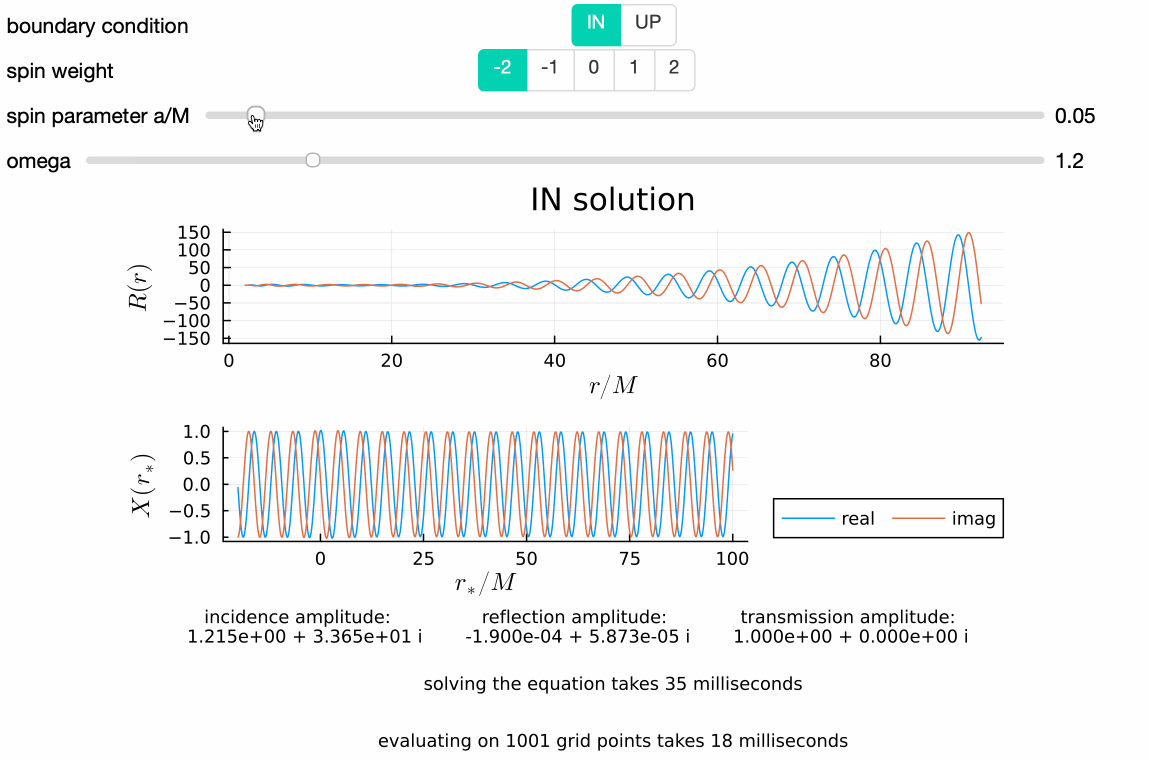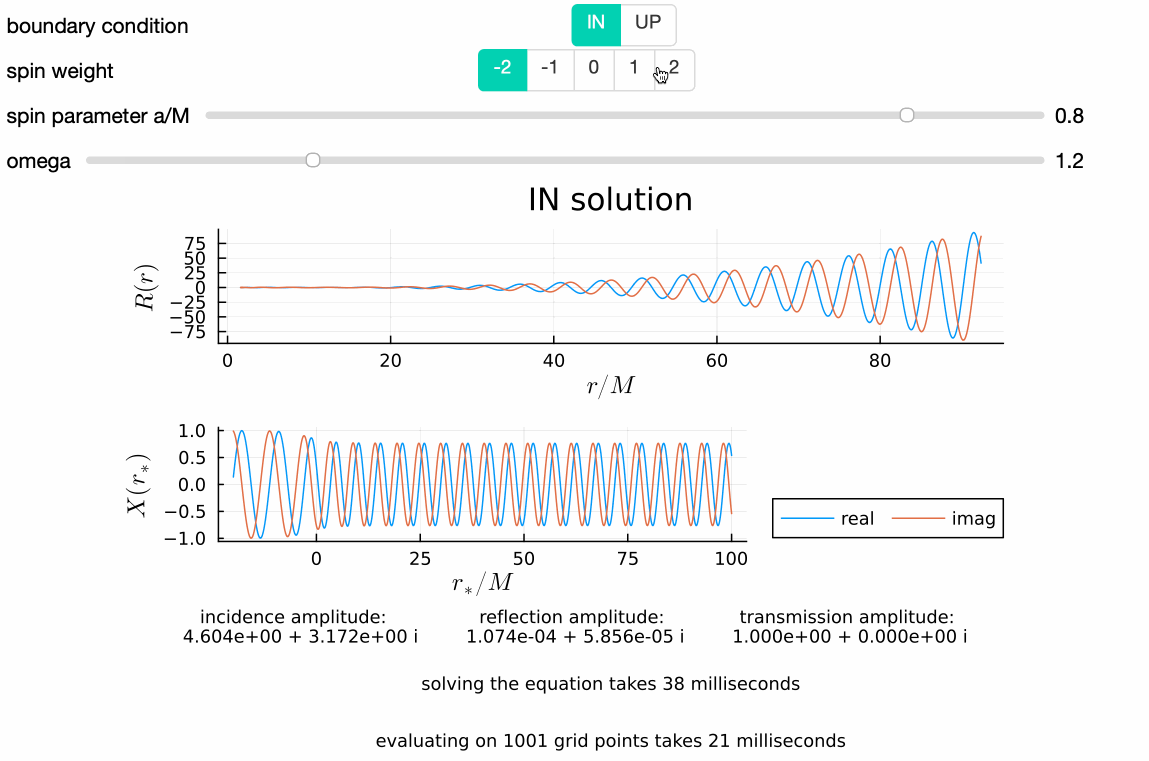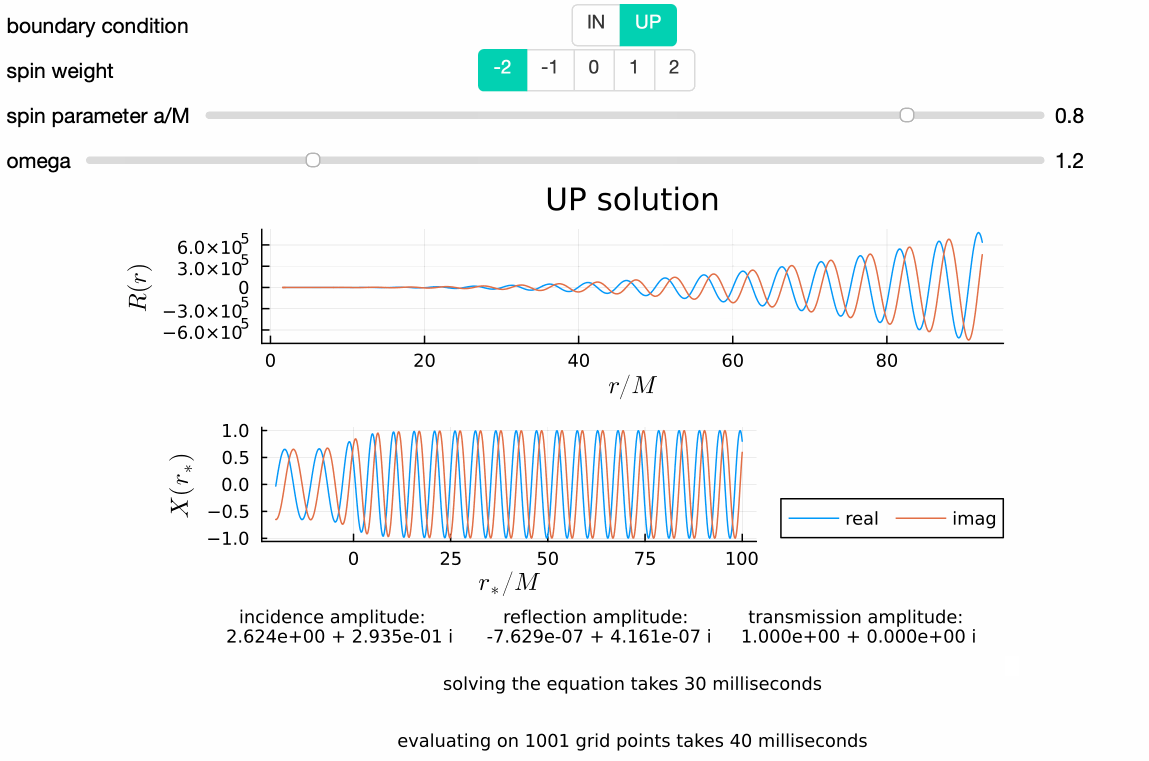
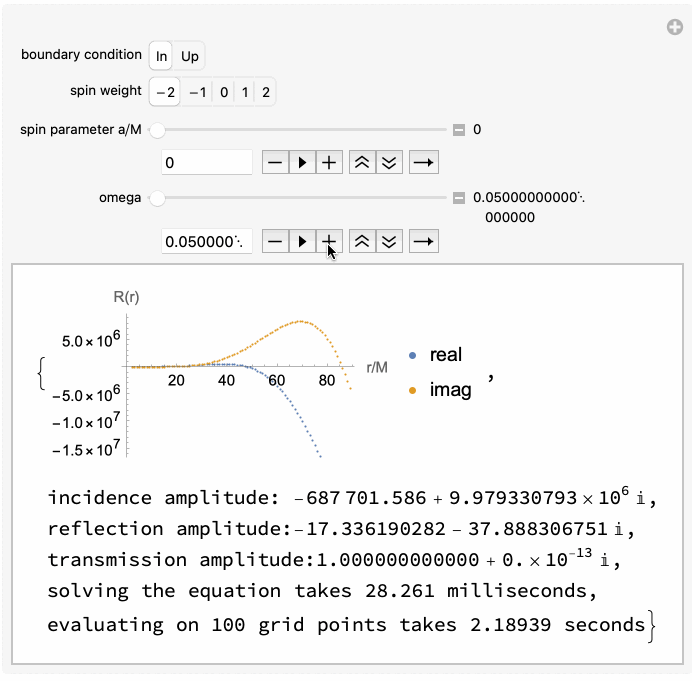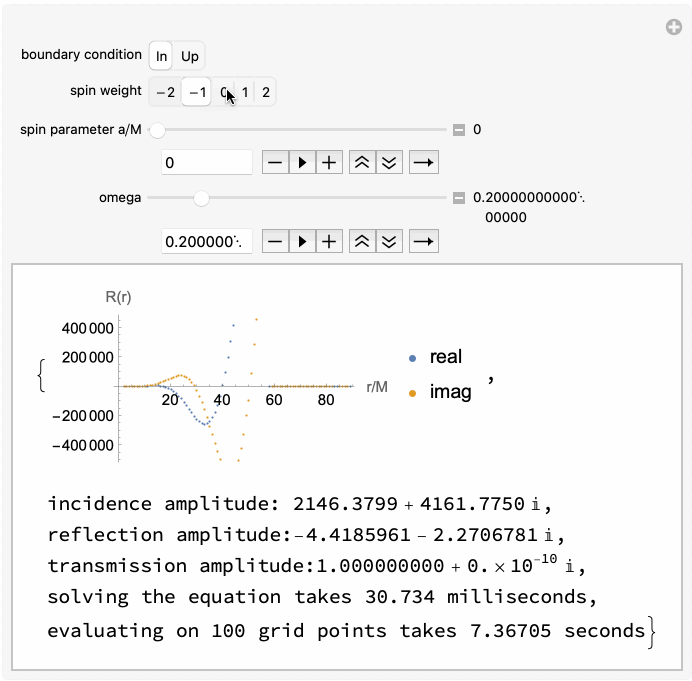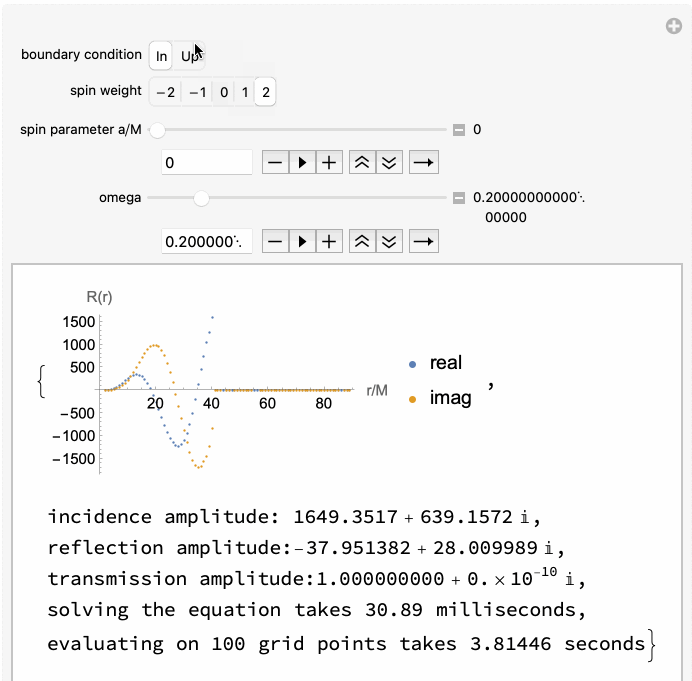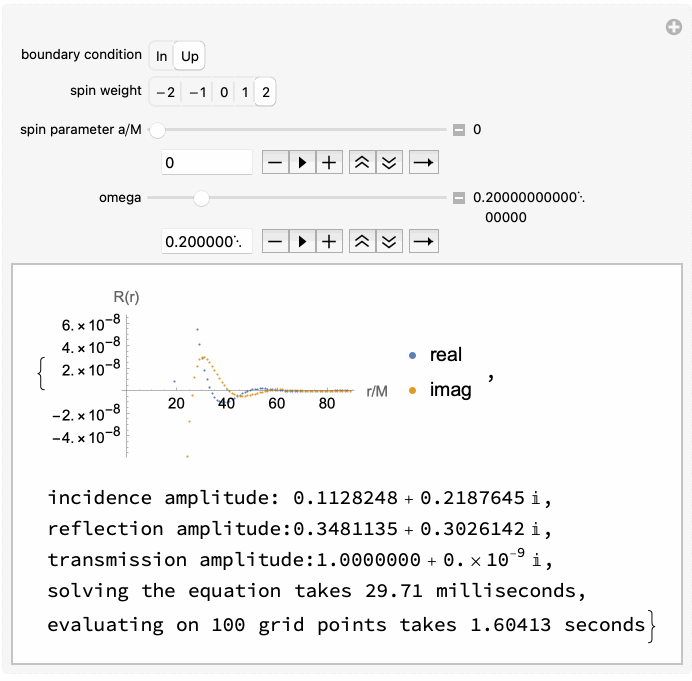
GeneralizedSasakiNakamura.jl

GeneralizedSasakiNakamura.jl computes solutions to the frequency-domain radial Teukolsky equation with the Generalized Sasaki-Nakamura (GSN) formalism.

The code is capable of handling both in-going and out-going radiation of scalar, electromagnetic, and gravitational type (corresponding to spin weight of $s = 0, \pm 1, \pm 2$ respectively).

The angular Teukolsky equation is solved with an accompanying julia package SpinWeightedSpheroidalHarmonics.jl using a spectral decomposition method.

To install the package using the Julia package manager, simply type the following in the Julia REPL:

using Pkg
Pkg.add("GeneralizedSasakiNakamura")

Note: There is no need to install SpinWeightedSpheroidalHarmonics.jl separately as it should be automatically installed by the package manager.

Works well at both low and high frequencies, and takes only a few tens of milliseconds on average:

(There was no caching! We solved the equation on-the-fly! The notebook generating this animation can be found here)

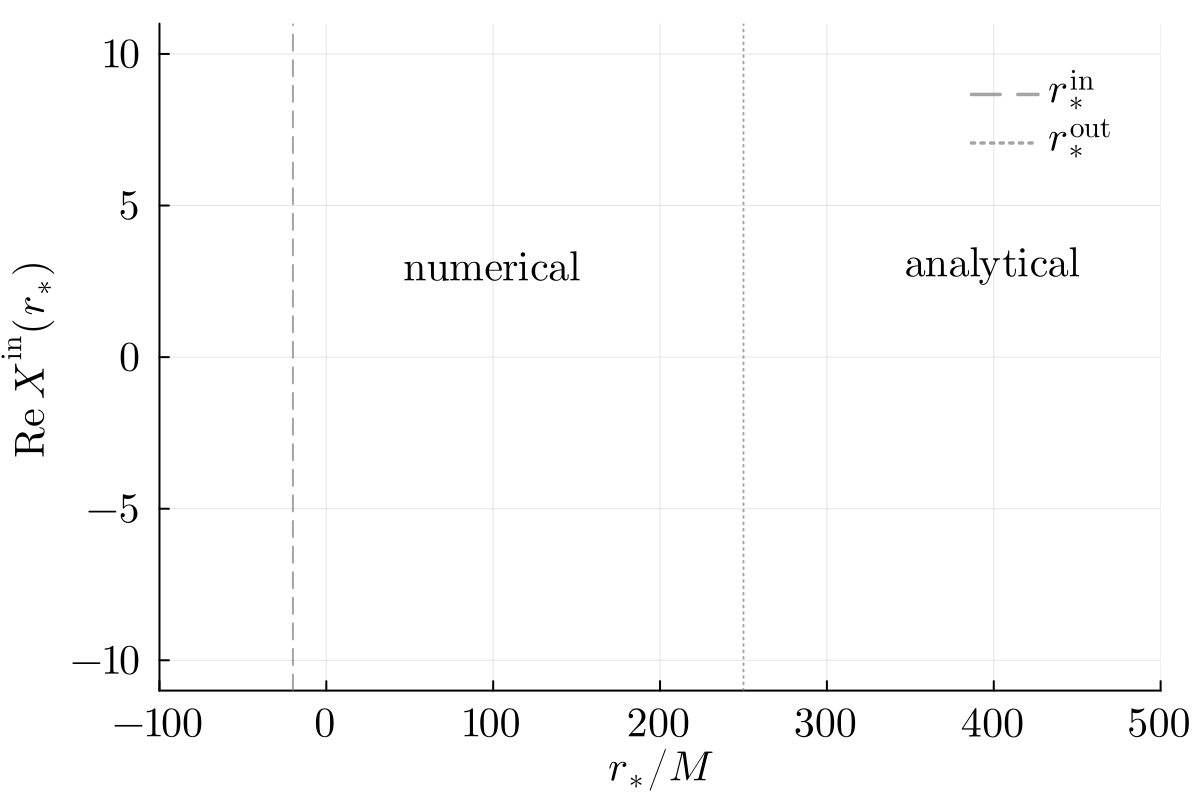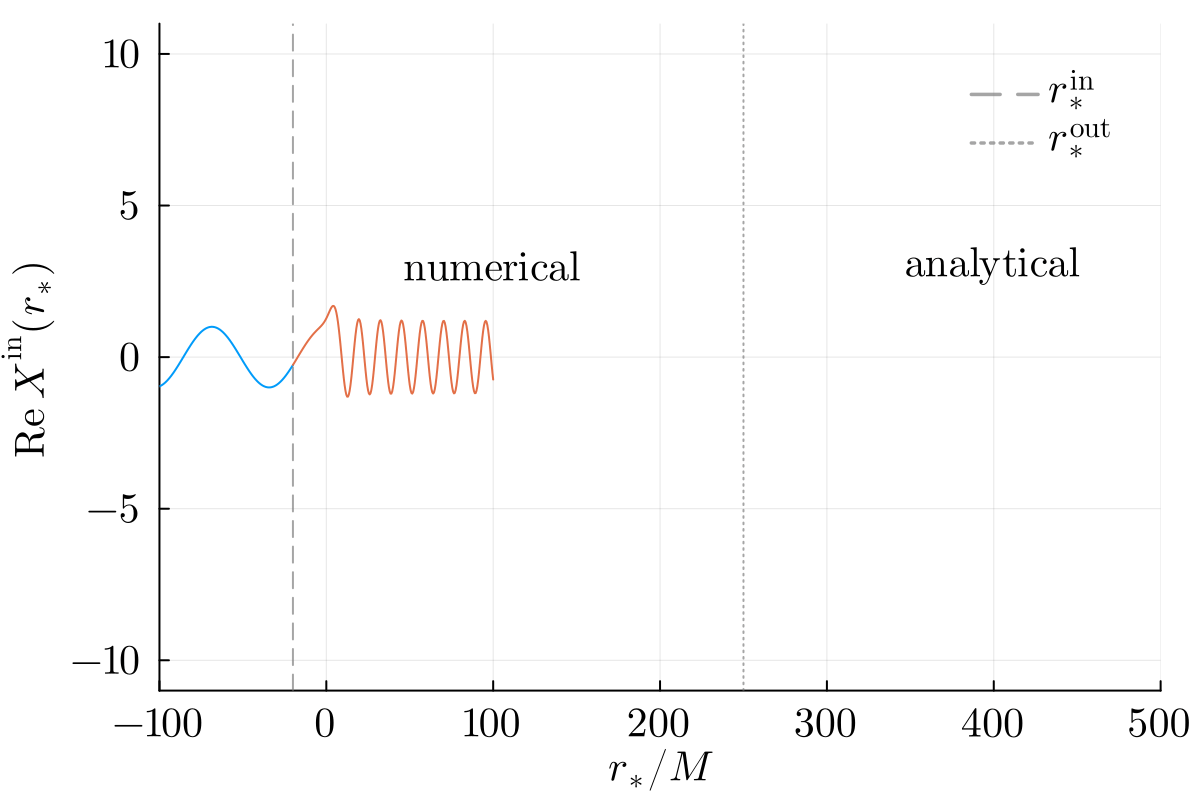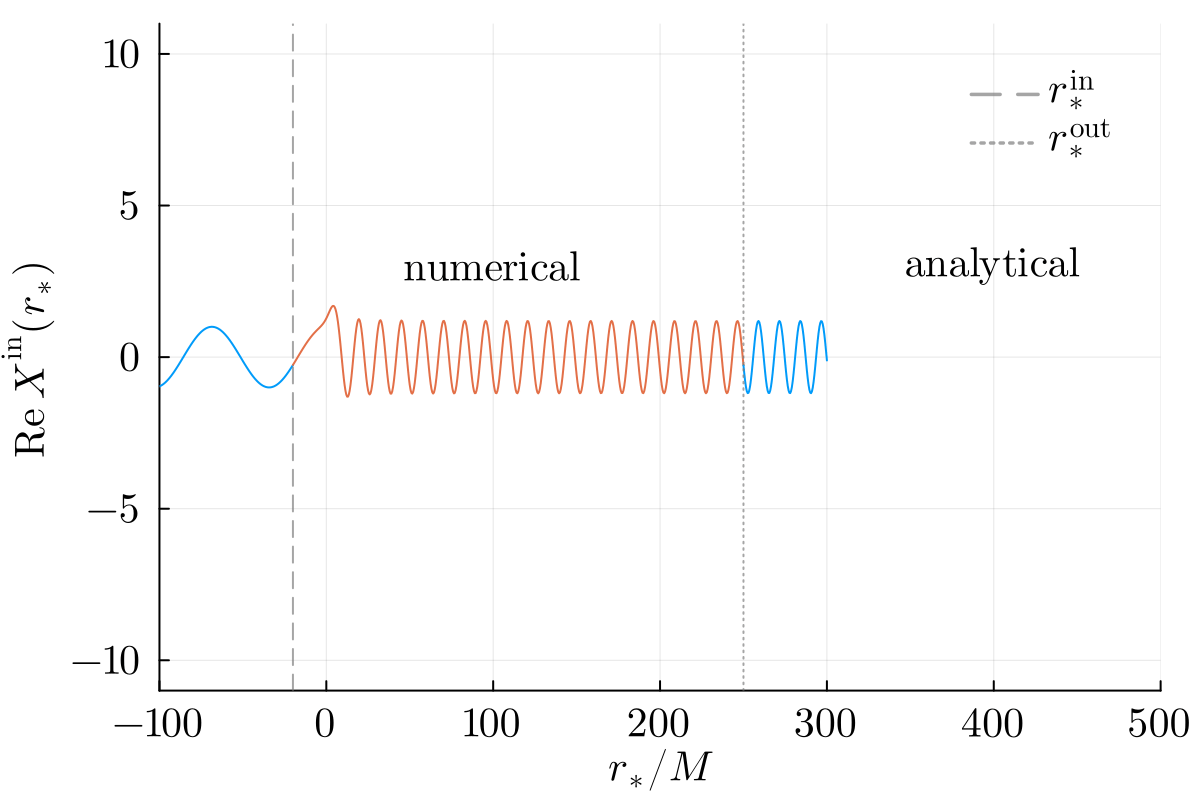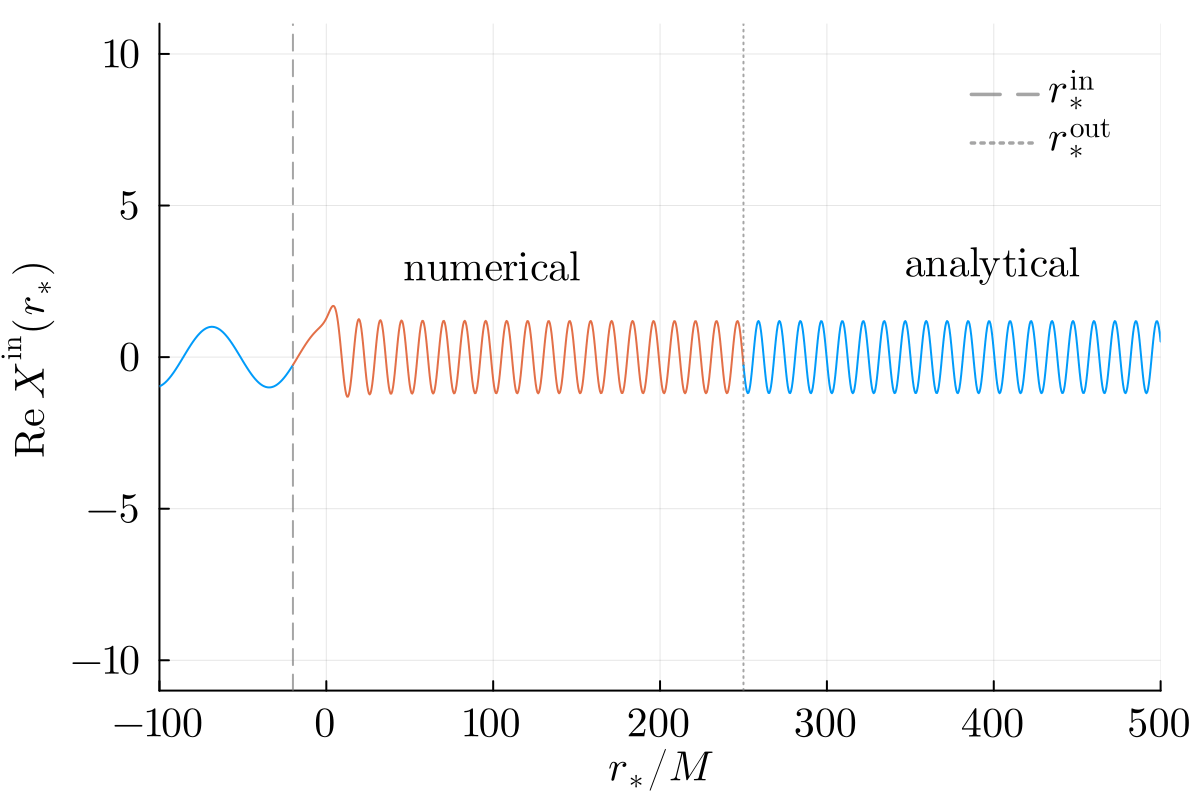
Numerical solutions are smoothly stitched to analytical ansatzes near the horizon and infinity at user-specified locations rsin and rsout respectively:

The following code snippet lets you solve the (source-free) Teukolsky function (in frequency domain) for the mode $s=-2, \ell=2, m=2, a=0.7, \omega=0.5$ that satisfies the purely-ingoing boundary condition at the horizon:

using GeneralizedSasakiNakamura # This is going to take some time to pre-compile, mostly due to DifferentialEquations.jl

# Specify which mode and what boundary condition
s=-2; l=2; m=2; a=0.7; omega=0.5; bc=IN;
# Specify where to match to ansatzes
rsin=-20; rsout=250;

# NOTE: julia uses 'just-ahead-of-time' compilation. Calling this the first time in each session will take some time
R = Teukolsky_radial(s, l, m, a, omega, bc, rsin, rsout) 

That's it! If you run this on Julia REPL, it should give you something like this

TeukolskyRadialFunction(
    mode=Mode(s=-2, l=2, m=2, a=0.7, omega=0.5, lambda=1.6966094016353415),
    boundary_condition=IN,
    transmission_amplitude=1.0 + 0.0im,
    incidence_amplitude=6.536587661197995 - 4.941203897068852im,
    reflection_amplitude=-0.128246619129379 - 0.44048133496664404im,
    normalization_convention=UNIT_TEUKOLSKY_TRANS
)

For example, if we want to evaluate the Teukolsky function at the location $r = 10M$, simply do

R(10)

This should give

77.57508416832009 - 429.40290952257226im

If you have used this code in your research that leads to a publication, please cite the following article:

@article{Lo:2023fvv,
    author = "Lo, Rico K. L.",
    title = "{Recipes for computing radiation from a Kerr black hole using Generalized Sasaki-Nakamura formalism: I. Homogeneous solutions}",
    eprint = "2306.16469",
    archivePrefix = "arXiv",
    primaryClass = "gr-qc",
    month = "6",
    year = "2023"
}

The package is licensed under the MIT License.