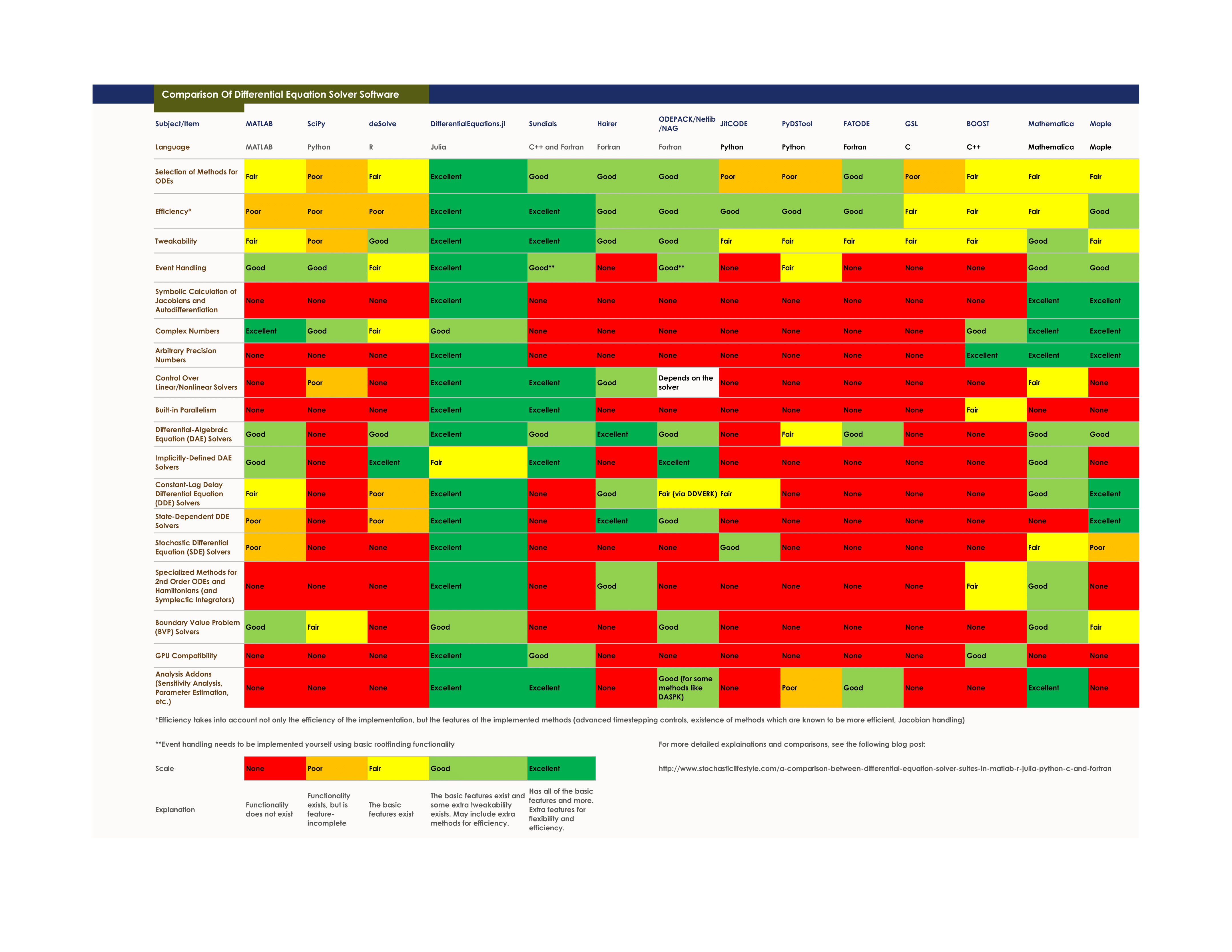
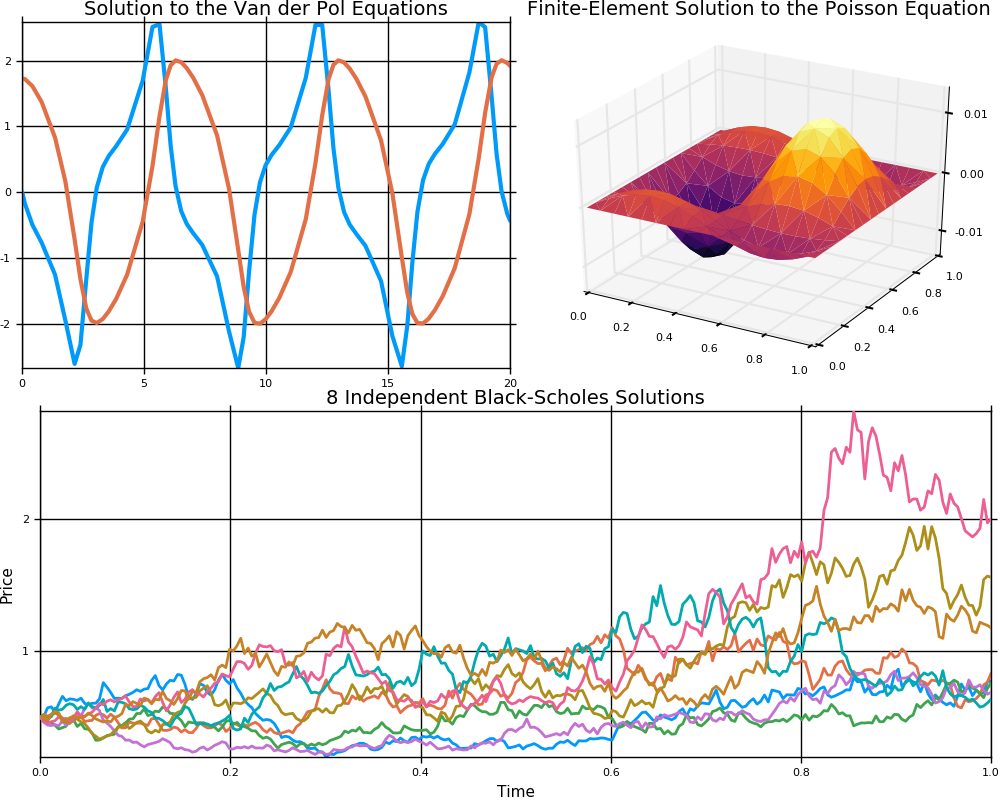
This is a suite for numerically solving differential equations written in Julia and available for use in Julia, Python, and R. The purpose of this package is to supply efficient Julia implementations of solvers for various differential equations. Equations within the realm of this package include:
- Discrete equations (function maps, discrete stochastic (Gillespie/Markov) simulations)
- Ordinary differential equations (ODEs)
- Split and Partitioned ODEs (Symplectic integrators, IMEX Methods)
- Stochastic ordinary differential equations (SODEs or SDEs)
- Stochastic differential-algebraic equations (SDAEs)
- Random differential equations (RODEs or RDEs)
- Differential algebraic equations (DAEs)
- Delay differential equations (DDEs)
- Neutral, retarded, and algebraic delay differential equations (NDDEs, RDDEs, and DDAEs)
- Stochastic delay differential equations (SDDEs)
- Experimental support for stochastic neutral, retarded, and algebraic delay differential equations (SNDDEs, SRDDEs, and SDDAEs)
- Mixed discrete and continuous equations (Hybrid Equations, Jump Diffusions)
- (Stochastic) partial differential equations ((S)PDEs) (with both finite difference and finite element methods)
The well-optimized DifferentialEquations solvers benchmark as some of the fastest implementations of classic algorithms. It also includes algorithms from recent research which routinely outperform the "standard" C/Fortran methods, and algorithms optimized for high-precision and HPC applications. Simultaneously, it wraps the classic C/Fortran methods, making it easy to switch over to them whenever necessary. Solving differential equations with different methods from different languages and packages can be done by changing one line of code, allowing for easy benchmarking to ensure you are using the fastest method possible.
DifferentialEquations.jl integrates with the Julia package sphere with:
- GPU acceleration through CUDA.jl and DiffEqGPU.jl
- Automated sparsity detection with Symbolics.jl
- Automatic Jacobian coloring with SparseDiffTools.jl, allowing for fast solutions to problems with sparse or structured (Tridiagonal, Banded, BlockBanded, etc.) Jacobians
- Allowing the specification of linear solvers for maximal efficiency with LinearSolve.jl
- Progress meter integration with the Visual Studio Code IDE for estimated time to solution
- Automatic plotting of time series and phase plots
- Built-in interpolations
- Wraps for common C/Fortran methods like Sundials and Hairer's radau
- Arbitrary precision with BigFloats and Arbfloats
- Arbitrary array types, allowing the definition of differential equations on matrices and distributed arrays
- Unit checked arithmetic with Unitful
Additionally, DifferentialEquations.jl comes with built-in analysis features, including:
- Forward and Adjoint Sensitivity Analysis (Automatic Differentiation) for fast gradient computations
- Parameter Estimation and Bayesian Analysis
- Neural differential equations with DiffEqFlux.jl for efficient scientific machine learning (scientific ML) and scientific AI.
- Automatic distributed, multithreaded, and GPU Parallel Ensemble Simulations
- Global Sensitivity Analysis
- Uncertainty Quantification
This gives a powerful mixture of speed and productivity features to help you solve and analyze your differential equations faster.
For information on using the package, see the stable documentation. Use the in-development documentation for the version of the documentation which contains the unreleased features.
All of the algorithms are thoroughly tested to ensure accuracy via convergence tests. The algorithms are continuously tested to show correctness. IJulia tutorial notebooks can be found at DiffEqTutorials.jl. Benchmarks can be found at DiffEqBenchmarks.jl. If you find any equation where there seems to be an error, please open an issue.
If you have any questions, or just want to chat about solvers/using the package, please feel free to chat in the Gitter channel. For bug reports, feature requests, etc., please submit an issue. If you're interested in contributing, please see the Developer Documentation.
The software in this ecosystem was developed as part of academic research. If you would like to help support it, please star the repository, as such metrics may help us secure funding in the future. If you use SciML software as part of your research, teaching, or other activities, we would be grateful if you could cite our work. Please see our citation page for guidelines.