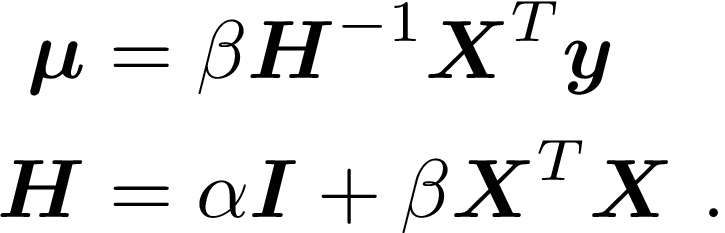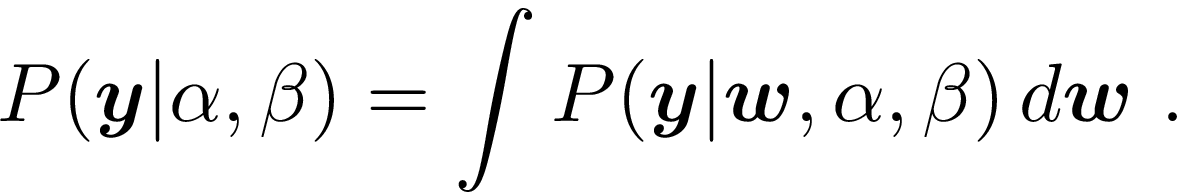BayesianLinearRegression

This library implements Bayesian Linear Regression, as described in Pattern Recognition and Machine Learning by Chris Bishop.

The idea is that if the weights are given iid normal prior distributions and the noise of the response vector is known (also iid normal), the posterior can be found easily in closed form. This leaves the question of how these values should be determined, and Bishop's suggestion is to use marginal likelihood.

The result of fitting such a model is a form that yields a posterior predictive distribution in closed form, and model evidence that can easily be used for model selection.

This package fits the linear regression model

Rather than finding “the” value for w, we take a Bayesian approach and find the posterior distribution, given by

where

All of the above depends on fixed values for α and β being specified in adviance. Alternatively, a “full Bayesian” approach would specify prior distributions over these, and work in terms of their posterior distribution for the final result.

Marginal likelihood finds a middle ground between these two approaches, and determines values for the \alpha and \beta hyperparameters by maximizing

This reduces to

This package maximizes the marginal likelihood using the approach described in Bishop (2006), which cycles through

1. Update α and β

2. Update H

3. Update μ

For details, see

Bishop, C. M. (2006). Pattern Recognition and Machine Learning (M. Jordan, J. Kleinberg, & B. Schölkopf (eds.); Vol. 53, Issue 9). Springer. Available online: https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf

First let's generate some fake data

using BayesianLinearRegression
n = 20
p = 7;
X = randn(n, p);
β = randn(p);
y = X * β + randn(n);

Next we instantiate and fit the model. fit! takes a callback keyword, which can be used to control stopping criteria, output some function of the model, or even change the model at each iteration.

julia> m = fit!(BayesianLinReg(X,y);
           callback = 
               # fixedEvidence()
               # stopAfter(2)
               stopAtIteration(50)
       );

Once the model is fit, we can ask for the log-evidence (same as the marginal likelihood):

julia> logEvidence(m)
-37.98301162730431

This can be used as a criterion for model selection; adding some junk features tends to reduce the log-evidence:

julia> logEvidence(fit!(BayesianLinReg([X randn(n,3)],y)))
-41.961261348171064

We can also query the values determined for the prior and the noise scales:

julia> priorScale(m)
1.2784615163925537

julia> noiseScale(m)
0.8520928089955583

The posteriorWeights include uncertainty, thanks to Measurements.jl:

julia> posteriorWeights(m)
7-element Array{Measurements.Measurement{Float64},1}:
 -0.35 ± 0.19
  0.07 ± 0.21
 -2.21 ± 0.29
  0.57 ± 0.22
  1.08 ± 0.18
 -2.14 ± 0.24
 -0.15 ± 0.25

This uncertainty is propagated for prediciton:

julia> predict(m,X)
20-element Array{Measurements.Measurement{Float64},1}:
   5.6 ± 1.0
  3.06 ± 0.95
 -3.14 ± 0.98
   3.3 ± 1.0
   4.6 ± 1.1
  -0.2 ± 1.0
 -0.91 ± 0.96
 -3.71 ± 0.99
  -4.0 ± 1.0
 -0.86 ± 0.95
 -5.69 ± 0.95
  4.32 ± 0.94
 -3.49 ± 0.94
  -0.7 ± 1.0
   0.5 ± 1.1
 -0.49 ± 0.92
  0.67 ± 0.91
  0.39 ± 0.95
  -7.3 ± 1.1
  0.11 ± 0.98

Finally, we can output the effective number of parameters, which is useful for some computations:

julia> effectiveNumParameters(m)
6.776655463465779