This package estimates linear models with high dimensional categorical variables and/or instrumental variables.

The package is registered in the General registry and so can be installed at the REPL with ] add FixedEffectModels.

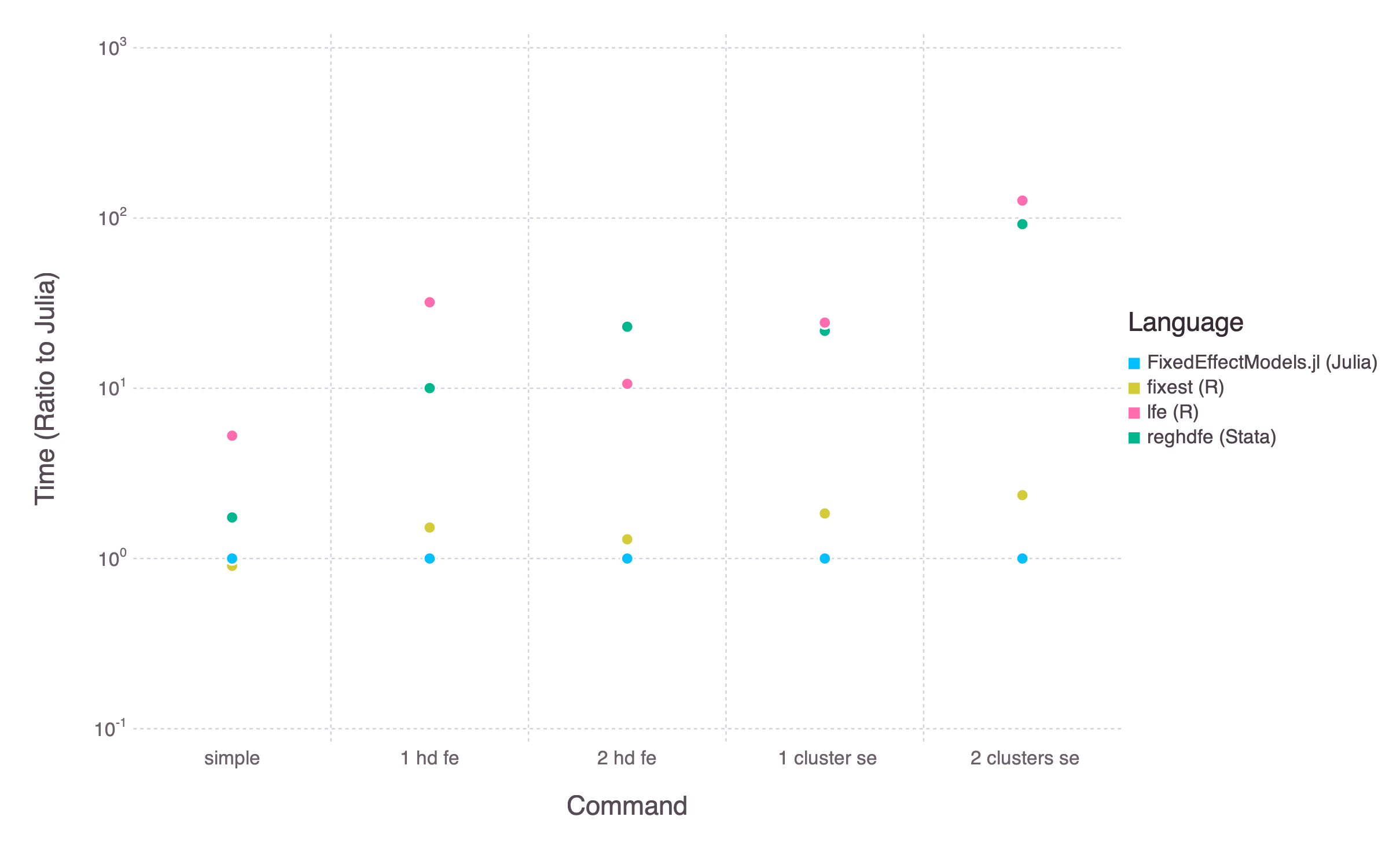
The objective of the package is similar to the Stata command reghdfe and the R packages lfe and fixest. The package is much faster than reghdfe or lfe. It also tends to be a bit faster than the more recent fixest (depending on the exact command). For complicated models, FixedEffectModels can also run on Nvidia GPUs for even faster performances (see below)

using DataFrames, RDatasets, FixedEffectModels
df = dataset("plm", "Cigar")
reg(df, @formula(Sales ~ NDI + fe(State) + fe(Year)), Vcov.cluster(:State), weights = :Pop)
#                             FixedEffectModel                            
# =========================================================================
# Number of obs:                 1380   Converged:                     true
# dof (model):                      1   dof (residuals):                 45
# R²:                           0.803   R² adjusted:                  0.798
# F-statistic:                13.3382   P-value:                      0.001
# R² within:                    0.139   Iterations:                       5
# =========================================================================
#         Estimate  Std. Error    t-stat  Pr(>|t|)   Lower 95%    Upper 95%
# ─────────────────────────────────────────────────────────────────────────
# NDI  -0.00526264  0.00144097  -3.65216    0.0007  -0.0081649  -0.00236038
# =========================================================================

• A typical formula is composed of one dependent variable, exogenous variables, endogenous variables, instrumental variables, and a set of high-dimensional fixed effects.

  dependent variable ~ exogenous variables + (endogenous variables ~ instrumental variables) + fe(fixedeffect variable)

  High-dimensional fixed effect variables are indicated with the function fe. You can add an arbitrary number of high dimensional fixed effects, separated with +. You can also interact fixed effects using & or *.

  For instance, to add state fixed effects use fe(State). To add both state and year fixed effects, use fe(State) + fe(Year). To add state-year fixed effects, use fe(State)&fe(Year). To add state specific slopes for year, use fe(State)&Year. To add both state fixed-effects and state specific slopes for year use fe(State)*Year.

  reg(df, @formula(Sales ~ Price + fe(State) + fe(Year)))
  reg(df, @formula(Sales ~ NDI + fe(State) + fe(State)&Year))
  reg(df, @formula(Sales ~ NDI + fe(State)&fe(Year)))              # for illustration only (this will not run here)
  reg(df, @formula(Sales ~ (Price ~ Pimin)))

  To construct formula programmatically, use

  reg(df, term(:Sales) ~ term(:NDI) + fe(:State) + fe(:Year))

• The option contrasts specifies that a column should be understood as a set of dummy variables:

   reg(df, @formula(Sales ~ Price + Year); contrasts = Dict(:Year => DummyCoding()))

  You can specify different base levels

   reg(df, @formula(Sales ~ Price + Year); contrasts = Dict(:Year => DummyCoding(base = 80)))

• The option weights specifies a variable for weights

   weights = :Pop

• Standard errors are indicated with the prefix Vcov (with the package Vcov)

   Vcov.robust()
   Vcov.cluster(:State)
   Vcov.cluster(:State, :Year)

• The option save can be set to one of the following: :none (default) to save nothing, :residuals to save residuals, :fe to save fixed effects, and :all to save both. Once saved, they can then be accessed using residuals(m) or fe(m) where m is the estimated model (the object returned by the function reg). Both residuals and fixed effects are aligned with the original dataframe used to estimate the model.

• The option method can be set to one of the following: :cpu, :CUDA, or :Metal (see Performances below).

reg returns a light object. It is composed of

• the vector of coefficients & the covariance matrix (use coef, coefnames, vcov on the output of reg)
• a boolean vector reporting rows used in the estimation
• a set of scalars (number of observations, the degree of freedoms, r2, etc)

Methods such as predict, residuals are still defined but require to specify a dataframe as a second argument. The problematic size of lm and glm models in R or Julia is discussed here, here, here here (and for absurd consequences, here and there).

You may use RegressionTables.jl to get publication-quality regression tables.

FixedEffectModels is multi-threaded. Use the option nthreads to select the number of threads to use in the estimation (defaults to Threads.nthreads()).

The package has an experimental support for GPUs. This can make the package an order of magnitude faster for complicated problems.

If you have a Nvidia GPU, run using CUDA before using FixedEffectModels. Then, estimate a model with method = :CUDA.

using CUDA, FixedEffectModels
@assert CUDA.functional()
df = dataset("plm", "Cigar")
reg(df, @formula(Sales ~ NDI + fe(State) + fe(Year)), method = :CUDA)

The package also supports Apple GPUs with Metal.jl, although I could not find a way to get better performance

using Metal, FixedEffectModels
@assert Metal.functional()
df = dataset("plm", "Cigar")
reg(df, @formula(Sales ~ NDI + fe(State) + fe(Year)), method = :Metal)

Denote the model y = X β + D θ + e where X is a matrix with few columns and D is the design matrix from categorical variables. Estimates for β, along with their standard errors, are obtained in two steps:

1. y, X are regressed on D using the package FixedEffects.jl
2. Estimates for β, along with their standard errors, are obtained by regressing the projected y on the projected X (an application of the Frisch Waugh-Lovell Theorem)
3. With the option save = true, estimates for the high dimensional fixed effects are obtained after regressing the residuals of the full model minus the residuals of the partialed out models on D using the package FixedEffects.jl

Baum, C. and Schaffer, M. (2013) AVAR: Stata module to perform asymptotic covariance estimation for iid and non-iid data robust to heteroskedasticity, autocorrelation, 1- and 2-way clustering, and common cross-panel autocorrelated disturbances. Statistical Software Components, Boston College Department of Economics.

Correia, S. (2014) REGHDFE: Stata module to perform linear or instrumental-variable regression absorbing any number of high-dimensional fixed effects. Statistical Software Components, Boston College Department of Economics.

Fong, DC. and Saunders, M. (2011) LSMR: An Iterative Algorithm for Sparse Least-Squares Problems. SIAM Journal on Scientific Computing

Gaure, S. (2013) OLS with Multiple High Dimensional Category Variables. Computational Statistics and Data Analysis